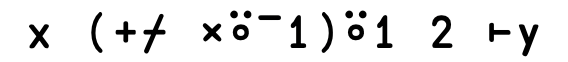The At operator: @
Contents
The At operator: @#
Once you understand how to write a program get someone else to write it. –Alan Perlis
Let’s look at the powerful immutable array update operator, At (@). By “immutable”, in this context, we mean non-destructive – it creates a new array, rather than mutating in place. Immutability is a good thing.
The dyadic @ operator has a lot of moving parts, and we won’t cover all possible combinations here.
References for @:
APL Cart has loads of examples
The APL Cultivations covered it under Primitive operators
Dyalog docs
Our usual prelude:
⎕IO ← 0
]box on
]rows on
@ can take both functions and arrays as either operand. In its simplest form, the left operand specifies values, and the right operand indices:
0@1 2 3⊢1 1 1 1 1 1 1
Recall from the introduction to operators that an operator returns a derived function. We inserted a Right tack to make clear the distinction – to stop stranding – between the operator’s right operand and the derived function’s argument. We could equally well have written:
(0@1 2 3) 1 1 1 1 1 1 1
We can think of the right operand as defining a selection criteria. For example, it can be a function that when called with the derived function’s argument returns a Boolean array:
'*'@{0 1 1 1 0 0 0 0 0 0 0} 'Hello world' ⍝ Right operand: function returning Boolean array
The left operand is either an array providing the new values for every value selected by the right argument, or a function which will be called with each selected element to produce the replacement value. For example, let’s add 5 to every even element:
{5+⍵}@{0=2|⍵} ⍳12
In this case, the right operand is the function {0=2|⍵}, which is called as such:
{0=2|⍵} ⍳12 ⍝ Return Boolean mask indicating the even numbers
The selected numbers are then:
({0=2|⍵} ⍳12)/⍳12 ⍝ Compress
which are passed to the left operand:
{5+⍵} 0 2 4 6 8 10 ⍝ Left operand applied to elements selected by right operand
Finally, @ will make the substitution.
Let’s write our own naive, overly verbose, partial implementation of @ for illustrative purposes.
]dinput
_At_ ← { ⍝ Partial @ - left and right operands must be functions, and the right arg a vector
mutator ← ⍺⍺ ⍝ Left operand -- function only
selector ← ⍵⍵ ⍝ Right operand -- function only
data ← ⍵ ⍝ Derived function right argument -- vector only. Note: copy
mask ← selector data
selection ← mask/data ⍝ Compress the data according to boolean mask
newvals ← mutator selection ⍝ Mutate our selection
(mask/data) ← newvals ⍝ Replace with the mutated values in copy
data ⍝ Return result
}
{5+⍵}_At_{0=2|⍵} ⍳12
We can shrink that down a bit without any real loss of clarity:
]dinput
_At_ ← { ⍝ Partial @ - left and right operands must be functions, and the right arg a vector
data ← ⍵
(mask/data) ← ⍺⍺ (mask←⍵⍵ ⍵)/⍵
data
}
{5+⍵}_At_{0=2|⍵} ⍳12
We used leading and trailing underscores when naming our operator to indicate visually that it’s a dyad, as suggested by Adám Brudzewsky’s unofficial style guide.
Higher rank: choose and reach#
The real @ has many more tricks up its sleeve, of course. It can also be applied to arrays of any rank, not just vectors.
If we look at Dyalog’s specification of @ we have
R←{X}(f@g)Y
If g is a simple vector, it chooses major cells in Y. If g is nested, it specifies indices for choose or reach indexing. What does that mean, then? One way to think of it is that the g vector behaves just as if it had been inserted between square brackets.
The first case is straightforward: the major cells of an array are those given by the first axis of the shape. In the case of a 2D matrix, its rows:
-@0 2 ⊢ 3 3⍴1 2 3 4 5 6 7 8 9 ⍝ Negate rows 0 and 2: major cells
If we want to access individual elements we can use choose indexing – which is a nested vector of indices:
-@(0 0)(2 2) ⊢ 3 3⍴1 2 3 4 5 6 7 8 9 ⍝ Negate corners of main diagonal by choose indexing
We can also access elements that are deeply nested using reach indexing, which we met briefly in the indexing section:
⎕ ← G ← 2 3⍴('Adam' 1)('Bob' 2)('Carl' 3)('Danni' 4)('Eve' 5)('Frank' 6)
'***' ¯999@((0 0)0)((1 2)1)⊢G
Examples#
Here’s a random collection of handy @ expressions. Many more on APLCart, too.
Replace dashes with spaces
' '@(=∘'-') 'Hello-World-One-Two'
Pad an array with zeros
{⍵@(1+⍳⍴⍵)⊢0⍴⍨2+⍴⍵} 2 2⍴1 1 1 1
Array search and replace
]DISPLAY array ← ?10 3⍴10
]DISPLAY 1 2 3 4 {⍺⍺(⍵⍵⌷⍨∘⊂⍳)@(∊∘⍺⍺)⍵} 0 10 100 1000 ⊢ array
Boolean alternating selection
Here’s a creative use of @ that Adám Brudzewsky posted on APL Orchard.
Given two arrays A, B and a boolean filter C, select items from A where C is false and from B where C is true:
A ← 1 2 3 4
B ← 11 22 33 44
C ← 0 1 0 1
(C/⍥,B)@{C}A
If that looks puzzling (we haven’t met the ⍥ operator yet!), for vectors, it’s just
(C/B)@{C}A
All that says is: replace the true spots (as defined by C) in A with the true spots (as defined by C) from B, which we could also do as an assignable indexing expression if we don’t mind mutating A:
(C/A) ← C/B
A