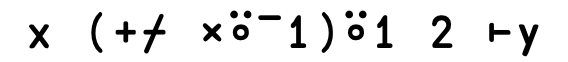Trainspotting

Simplicity and elegance are unpopular because they require hard work and discipline to achieve and education to be appreciated. – Edsger Dijkstra

Tacit is the third way to write code in Dyalog APL, after dfns, and traditional (which we’re not covering). The tacit style, also sometimes called point-free, was taken from the J language, which originated the concept. Tacit code can be made super-terse, and is best reserved for short snippets only. APL idioms – short, efficient, and ultra-optimised bits of code, are often expressed in tacit. You’ll find that pretty much everything on APLCart is written in tacit, and as you start working on improving your Code Golf handicap, tacit is an essential skill.

We can look at tacit programming in APL as a little embedded DSL for functional composition, complete with its own grammar. The rules of this grammar are actually quite simple, but learning how to read and write tacit functions takes a lot of practice, even for those well-versed in the rest of APL.

References for tacit programming:

• APL Wiki

• Cultivation

• Dyalog webinar

• dfns page on dfn to tacit translation

The word tacit means implicit, and refers to a function where there is no explicit mention of its arguments. In a tacit function, then, you’ll see no ⍺ and ⍵ as you would in a dfn. Instead a set of rules decide how the components of a tacit function interact with the arguments.

This time, in our prelude, we’ll use the -trains=tree -fns=on arguments to ]box which helps with showing the structure of tacit functions.

⎕IO ← 0
]box on -style=min -trains=tree -fns=on
]rows on
assert←{⍺←'assertion failure' ⋄ 0∊⍵:⍺ ⎕signal 8 ⋄ shy←0}

Was ON -style=min -trains=tree -fns=on

Was OFF

The tacit rules: atop

A tacit function is wrapped in parentheses, ( ... ), and is governed by a set of rules. Let’s begin with the easiest one, the monadic atop. An atop, also known as a 2-train, is a combination of two functions:

(f g)Y → f g Y

This states that the tacit function (f g), comprising the monadic functions f and g, simply corresponds to the sequence f g applied to an argument array Y. Well, that seems… obvious? We can try it:

⎕ ← Y ← 3 3⍴⍳9
(-⍉)Y ⍝ Tacit
-⍉Y   ⍝ Explicit "beside"

0 1 2
3 4 5
6 7 8

 0 ¯3 ¯6
¯1 ¯4 ¯7
¯2 ¯5 ¯8

 0 ¯3 ¯6
¯1 ¯4 ¯7
¯2 ¯5 ¯8

Yes, it’s understandable if you’re scratching your head, wondering “what’s the point of that then?”. It pays to think of it as a means of creating a derived function. Doing

-⍉Y

is two operations, whereas

(-⍉)Y

is the application of a single, derived function.

But the main purpose of the monadic atop rule is to serve as a building block in more complex tacit functions, as we shall discover shortly.

Let’s move on to the dyadic version of atop instead:

X (f g) Y → f X g Y

Here, the dyadic tacit function (f g) combines the monadic function f and the dyadic function g. Let’s say we want to tally the elements that are left if you remove all elements from array A from those in B:

B ← 1 2 3 4 5 6 7
A ← 3 2 6
≢ B ~ A

4

There we can see the f X g Y pattern. Let’s try the tacit version, a dyadic atop:

B (≢~) A

4

There’s also a monadic version of the atop rule:

(f g)Y → f g Y

Again, hard to see the utility yet, perhaps.

The tacit rules: fork

Let’s keep going! Here’s our first fork (also known as a 3-train) – a tacit combination of three functions:

X (f g h) Y → (X f Y) g (X h Y)

This is perhaps the simplest tacit rule that one can see applications for. Consider the three-way compare (sometimes called “spaceship”) operator, a <=> b that some languages (like Perl or Ruby) offer. It returns a negative value if a < b, 0 if a == b and a positive value if a > b. APL has no such thing, but we can cook up a tacit function using the fork rule:

cmp ← >-<

1 cmp 2
1 cmp 1
2 cmp 1

¯1

0

1

Let’s look at the rule application to see why it works:

(a > b) - (a < b) ⍝ using the fork rule: (X f Y) g (X h Y)

Once you learn to see this pattern, it really crops up frequently. Why is it called a “fork”? Well, if we have specified ]box on with -trains=tree we can ask the interpreter to show us its parse of the tacit function:

cmp

┌─┼─┐
> - <

Very much a fork, or trident. As an aside, you can actually achieve the same thing with one symbol fewer:

cmp ← ×- ⍝ Try it!

Let’s look at a few more examples. A common problem is to split a string into substrings, dividing on some separator character. Here’s one way you can achieve that, using a dfn:

Split ← {⍵⊆⍨⍺≠⍵}

' ' Split 'A common problem is to split a string into substrings'

┌─┬──────┬───────┬──┬──┬─────┬─┬──────┬────┬──────────┐
│A│common│problem│is│to│split│a│string│into│substrings│
└─┴──────┴───────┴──┴──┴─────┴─┴──────┴────┴──────────┘

Let’s rework that into a tacit formulation instead, taking it step by step. First, let’s flip that selfie and put in some parentheses for emphasis:

Split ← {(⍺≠⍵) ⊆ (⍵)}

So that almost matches the fork pattern (X f Y) g (X h Y), but not quite. The last part makes no reference to ⍺. Let’s address that with a tack-trick:

Split ← {(⍺≠⍵) ⊆ (⍺⊢⍵)}

To recap, the tacks (⊣⊢) are functions that just return the value they’re “pointing” to:

2⊢3
⊢5
2⊣3

3

5

2

They are very useful when writing tacit functions, as we’ve just seen. We now have a dfn body that matches the fork rule, and we can write it tacitly as:

Split ← ≠⊆⊢

' ' Split 'It should still work the same way'

┌──┬──────┬─────┬────┬───┬────┬───┐
│It│should│still│work│the│same│way│
└──┴──────┴─────┴────┴───┴────┴───┘

Ok, let’s try another one, this time going the other way. Here’s a fork that scales a vector of numbers such that its components sum to 1:

UnitSum ← ⊢÷+/

UnitSum 1 2 3 4 5 6

0.04761904762 0.09523809524 0.1428571429 0.1904761905 0.2380952381 0.2857142857

What is the corresponding explicit dfn?

The complication here is that we now have an operator involved: a reduction. Recall that operators take one (or two) function(s) and return a derived function that can then be applied to arguments in turn. So let’s think of the sum-reduction as a single function. Using spaces to make this clearer we get:

UnitSum ← ⊢ ÷ +/

We know already that the fork itself is monadic, meaning that the f and the h functions must both be monadic, and the g function dyadic. The tack becomes just ⍵ and the sum-reduction we just need to give an argument:

UnitSum ← {⍵÷+/⍵}

UnitSum 1 2 3 4 5 6

0.04761904762 0.09523809524 0.1428571429 0.1904761905 0.2380952381 0.2857142857

That last example – a monadic fork – can be formalised as:

(f g h)Y → (f Y) g (h Y)

There are, in fact, two more fork-varieties, beyond the two we’ve already seen. They differ in how the consitutent functions are applied (monadically or dyadically):

X(Z g h)Y → Z g X h Y ⍝ h dyad, g dyad, derived dyad
(X g h)Y  → X g h Y   ⍝ h modad, g dyad, derived monad

Summary: forks and atops

For completeness, then – here are all the rules of the tacit grammar in one place:

Tacit	Type	Explicit
X(Z g h)Y	Fork	Z g X h Y
X(f g h)Y	Fork	(X f Y) g (X h Y)
(X g h)Y	Fork	X g h Y
(f g h)Y	Fork	(f Y) g (h Y)
X(f g)Y	Atop	f X g Y
(f g)Y	Atop	f g Y

Forks atop forks

This is where the real fun begins. We can string together longer tacit functions by combining forks and atops. Some consideration should be given to comprehensibility here. Long stretches of tacit code requires more effort to understand than the corresponding explicit formulation.

As our tacit rules indicate, barring the presence of parentheses, a combination of three functions is a fork, and two functions is an atop. If we have more than three functions, we start reading from the right, making groups of threes and twos, and combine those using the fork and atop rules.

From Dyalog’s docs:

…in the absence of parentheses, a sequence of an odd number of functions resolves to a 3-train (fork) and an even-numbered sequence resolves to a 2-train (atop)

So how long is too long a train? It depends on the “carriages”. The example given in Dyalog’s docs above is a good point:

6 (⌽+,-,×,÷) 2

3 12 4 8

That’s 8 constituent functions. We’ll prise it apart in a bit, but looking at it, it’s pretty clear what the intention is: find the sum, difference, product and ratio of two numbers, and reverse the list.

As always, let’s look at the parse:

⌽+,-,×,÷

┌─┴─┐
⌽ ┌─┼───┐
  + , ┌─┼───┐
      - , ┌─┼─┐
          × , ÷

So reading right to left, down to up, we have three forks and an atop. Let’s resolve them from the right:

f1 ← ×,÷ ⍝ ...fork, (6×2),(6÷2)

⎕ ← r ← 6 (⌽+,-,f1) 2 ⍝ does it still work?
assert r≡6 (⌽+,-,×,÷) 2

3 12 4 8

The next fork is now

f2 ← -,f1 ⍝ ...fork: (6-2),f1 → (6-2),(6×2),(6÷2)

6 (⌽+,f2) 2 

3 12 4 8

and the final fork is more of the same:

f3 ← +,f2 ⍝ (6+2),(6-2),(6×2),(6÷2)

6 (⌽f3) 2 

3 12 4 8

And finally, the atop, which moves the left argument to between the functions and removes the brackets:

⌽ 6 f3 2

3 12 4 8

or, fully explicit:

6 {⌽(⍺+⍵),(⍺-⍵),(⍺×⍵),⍺÷⍵} 2

3 12 4 8

Complicating factors

Using the method outlined above, you can usually untangle reasonably-sized trains that others have composed:

• Use ]box on -style=mid -trains=tree -fns=on to visualise the parse tree for the train

• Follow the pattern indicated by the tree, and resolve forks and atops (R→L) using The Rules

However, certain factors make this more complicated:

• Mid-train parentheses to alter order of precedence

• Binding strengths – operators bind tighter than functions

• Jots & tacks, if overused.

A handy tacit function is finding the min and max of an array, which we can use to demonstrate the operator binding:

minmax ← ⌊/,⌈/
minmax 7 2 3 8 0 9 12

0 12

This is a single fork:

minmax

  ┌─┼─┐
  / , /
┌─┘ ┌─┘
⌊   ⌈

So we can see that we need to start by letting the reduces bind first to form the derived functions that make up the fork. Ok, that wasn’t too bad. What about this one?

⎕ ← ones ← ⊢∧(∧⍀∨⍀=⊢) ⍝ Hat tip to Adám Brudzewski for the suggestion

┌─┼───┐
⊢ ∧ ┌─┴─┐
    ⍀ ┌─┼─┐
  ┌─┘ ⍀ = ⊢
  ∧ ┌─┘
    ∨

Top marks if you can say what that even does. Before we get into that, we can see that the parenthesis have affected the “groups of three from the right” parse. We’re now looking at a fork-atop-fork, two operators and two tacks. All non-specific religious holidays came at once.

This function preserves the first uninterrupted sequence of 1s in a vector:

ones 0 0 1 1 1 0 0 0 1 0 1 1 1 0

0 0 1 1 1 0 0 0 0 0 0 0 0 0

Let’s untangle the parse tree, bottom-up, right-left. The first fork is

⎕ ← f1 ← ∨⍀ = ⊢ ⍝ ...monadic fork, giving a dfn equivalent: {(∨⍀⍵)=⍵}

  ┌─┼─┐
  ⍀ = ⊢
┌─┘
∨

⎕ ← r ← (⊢∧(∧⍀f1)) 0 0 1 1 1 0 0 0 1 0 1 1 1 0
assert r≡ones 0 0 1 1 1 0 0 0 1 0 1 1 1 0 ⍝ still works!

0 0 1 1 1 0 0 0 0 0 0 0 0 0

Now let’s tackle the atop, which is just applying the and-scan to the fork:

⎕ ← a1 ← ∧⍀f1

  ┌─┴─┐
  ⍀ ┌─┼─┐
┌─┘ ⍀ = ⊢
∧ ┌─┘
  ∨

(⊢∧a1) 0 0 1 1 1 0 0 0 1 0 1 1 1 0

0 0 1 1 1 0 0 0 0 0 0 0 0 0

and there we have a monadic fork:

{⍵∧a1 ⍵} 0 0 1 1 1 0 0 0 1 0 1 1 1 0

0 0 1 1 1 0 0 0 0 0 0 0 0 0

We can now fully untangle it if we want:

{⍵∧∧⍀(∨⍀⍵)=⍵} 0 0 1 1 1 0 0 0 1 0 1 1 1 0

0 0 1 1 1 0 0 0 0 0 0 0 0 0

So now we can compare the tacit and explicit forms of the same function:

tacit ← ⊢∧(∧⍀∨⍀=⊢)
expl  ← {⍵∧∧⍀(∨⍀⍵)=⍵}

Which one is “better”? Yes, the tacit formulation is shorter by three glyphs. Readability is a slippery concept which depends on the skill and experience of the reader, but at least to this reader, without going through the above deconstruction exercise, I could not have told you how the tacit function worked. In the explicit formulation – to my eyes at least – the algorithm is more visible.

Let’s work through a couple more, back and forth. If you haven’t already, do check out Richard Park’s most excellent webinar on the topic, too.

Note

Working through examples this way, whilst somewhat tedious, is the only way to learn. Eventually it clicks. If this all feels a bit dry, skip to the next chapter and keep coming back here in small doses.

Here’s a tacit phrase which groups pairs of elements based on the first:

group ← ↓⊃¨,∘⊂⌸⊢/¨ ⍝ Group pairs based on first element
group ⎕←(5 3)(5 6)(7 5)(4 7)(1 8)(2 4)(1 2)

┌───┬───┬───┬───┬───┬───┬───┐
│5 3│5 6│7 5│4 7│1 8│2 4│1 2│
└───┴───┴───┴───┴───┴───┴───┘
┌───────┬─────┬─────┬───────┬─────┐
│┌─┬───┐│┌─┬─┐│┌─┬─┐│┌─┬───┐│┌─┬─┐│
││5│3 6│││7│5│││4│7│││1│8 2│││2│4││
│└─┴───┘│└─┴─┘│└─┴─┘│└─┴───┘│└─┴─┘│
└───────┴─────┴─────┴───────┴─────┘

Let’s look at the parse tree:

group

┌──┴──┐
↓ ┌───┼───┐
  ¨   ⌸   ¨
┌─┘ ┌─┘ ┌─┘
⊃   ∘   ⊢/
   ┌┴┐
   , ⊂

Yikes… but actually, it looks worse than it is – it’s a single fork, with an atop. The sprinkling of operators make it look more complicated than it is. So, bit by bit as indicated by the tree, starting with the Key (⌸):

key ← ⎕←,∘⊂⌸

   ⌸
 ┌─┘
 ∘
┌┴┐
, ⊂

Looks correct. If we substitute into the original definition, we get

↓⊃¨key⊢/¨

┌──┴──┐
↓ ┌───┼───┐
  ¨   ⌸   ¨
┌─┘ ┌─┘ ┌─┘
⊃   ∘   ⊢/
   ┌┴┐
   , ⊂

Yep. Still the same. Now for the left and right tines:

discloseAll ← ⊃¨
mergeLasts ← ⊢/¨
↓discloseAll key mergeLasts

┌──┴──┐
↓ ┌───┼───┐
  ¨   ⌸   ¨
┌─┘ ┌─┘ ┌─┘
⊃   ∘   ⊢/
   ┌┴┐
   , ⊂

We can now translate to a dfn:

{↓(discloseAll ⍵) key (mergeLasts ⍵)}  (5 3)(5 6)(7 5)(4 7)(1 8)(2 4)(1 2)

┌───────┬─────┬─────┬───────┬─────┐
│┌─┬───┐│┌─┬─┐│┌─┬─┐│┌─┬───┐│┌─┬─┐│
││5│3 6│││7│5│││4│7│││1│8 2│││2│4││
│└─┴───┘│└─┴─┘│└─┴─┘│└─┴───┘│└─┴─┘│
└───────┴─────┴─────┴───────┴─────┘

{↓(⊃¨⍵) ,∘⊂⌸ ⊢/¨⍵} (5 3)(5 6)(7 5)(4 7)(1 8)(2 4)(1 2)

┌───────┬─────┬─────┬───────┬─────┐
│┌─┬───┐│┌─┬─┐│┌─┬─┐│┌─┬───┐│┌─┬─┐│
││5│3 6│││7│5│││4│7│││1│8 2│││2│4││
│└─┴───┘│└─┴─┘│└─┴─┘│└─┴───┘│└─┴─┘│
└───────┴─────┴─────┴───────┴─────┘

The operand to Key is a derived function. We could expand that, too, if we want to be purist:

{↓(⊃¨⍵) {⍺,⊂⍵}⌸ ⊢/¨⍵} (5 3)(5 6)(7 5)(4 7)(1 8)(2 4)(1 2)

┌───────┬─────┬─────┬───────┬─────┐
│┌─┬───┐│┌─┬─┐│┌─┬─┐│┌─┬───┐│┌─┬─┐│
││5│3 6│││7│5│││4│7│││1│8 2│││2│4││
│└─┴───┘│└─┴─┘│└─┴─┘│└─┴───┘│└─┴─┘│
└───────┴─────┴─────┴───────┴─────┘

Here’s another one. What does this even do?

2 (|∘⍳∘≢⊢∘⊂⌸⊢) 'dyaloge'

┌────┬───┐
│daoe│ylg│
└────┴───┘

Another thing we can do that may or may not be useful is to ask the interpreter to give us a parethesised expression instead of the parse tree.

]box on -style=mid -trains=parens -fns=on

Was ON -style=mid -trains=parens -fns=on

|∘⍳∘≢⊢∘⊂⌸⊢

((|∘⍳)∘≢)((⊢∘⊂)⌸)⊢

Some say that’s an easier start than the tree. Take your pick. Following the steps above you should land on:

2 {(⍺|⍳≢⍵) {⊂⍵}⌸ ⍵} 'dyaloge'

┌→───┬───┐
│daoe│ylg│
└───→┴──→┘

This one draws a bar chart:

]DISPLAY (↑⍴¨∘'⎕')3 0 9 6 2 7 6

┌→────────┐
↓⎕⎕⎕      │
│         │
│⎕⎕⎕⎕⎕⎕⎕⎕⎕│
│⎕⎕⎕⎕⎕⎕   │
│⎕⎕       │
│⎕⎕⎕⎕⎕⎕⎕  │
│⎕⎕⎕⎕⎕⎕   │
└─────────┘

which is just

]DISPLAY ↑{⍵⍴'⎕'}¨3 0 9 6 2 7 6

┌→────────┐
↓⎕⎕⎕      │
│         │
│⎕⎕⎕⎕⎕⎕⎕⎕⎕│
│⎕⎕⎕⎕⎕⎕   │
│⎕⎕       │
│⎕⎕⎕⎕⎕⎕⎕  │
│⎕⎕⎕⎕⎕⎕   │
└─────────┘

Let’s try a couple of harder ones. This one removes leading, trailing and repeated stretches of ⍺ from ⍵:

trim ← 1↓,⊢⍤/⍨1(⊢∨⌽)0,≠
' ' trim '        hello     world     '

hello world

]box on -style=mid -trains=tree -fns=on ⍝ I'm a tree guy!

Was ON -style=mid -trains=tree -fns=on

trim

┌─┼───┐
1 ↓ ┌─┼─────┐
    , ⍨ ┌───┼─────┐
    ┌─┘ 1 ┌─┼─┐ ┌─┼─┐
    ⍤     ⊢ ∨ ⌽ 0 , ≠
   ┌┴┐
   ⊢ /

No fewer than five forks! The other thing to note is the use of ⍤ here which in fact is not Rank. When ⍤ is used with a right function operand, it becomes Atop, not Rank (which takes a right array operand).

The tacit phrase ⊢⍤f is a trick to force f to be parsed as a function, rather than as an operator for glyphs that can be either. In our case, ⊢⍤/⍨ is just {⍵/⍺}. With that we may be able to skip a few intermediate steps:

f ← {1{⍵∨⍺⌽⍵}⍺{0,⍺≠⍵}⍵}
g ← {⍵/⍺}     
trimdfn ← {1↓(⍺,⍵)g⍺f⍵}

' ' trimdfn '        hello     world     '

hello world

Expanding that out we can make a few simplifications, arriving at the resaonably compact

trim ← {1↓(x∨1⌽x←0,⍺≠⍵)/⍺,⍵}

' ' trim '        hello     world     '

hello world

How about going the other way? We’ve done some already. A pretty comprehensive guide to the mechanical process of translating a dfn to its tacit equivalent can be found in the docs for the dfns workspace, mentioned at the top of this chapter.

Here’s a noddy dfn that takes a string consisting of a leading letter and some digits, and returns a 2-element vector with the letter and the number:

{(1↑⍵),⍎1↓⍵} 'X1234'

X 1234

There’s clearly a fork in there, but also an atop. This should pose little difficulty, right? Change the braces for parantheses, and omegas for right-tack, but we need to delineate the eval call:

((1↑⊢),(⍎(1↓⊢))) 'X1234'

X 1234

We can do more here. Both left and right tines of the fork share a 1. We can make that a left argument, so in our case a left tack:

1 ((⊣↑⊢),(⍎(⊣↓⊢))) 'X1234'

X 1234

but the pattern ⊣f⊢ is just f, which also lets us remove some parentheses:

1 (↑,(⍎↓)) 'X1234'

X 1234

We can actually remove the inner parantheses, too, by a bit of sleight of hand:

1 (↑,∘⍎↓) 'X1234'

X 1234

but these two trains – whilst doing the same thing – parse differently:

↑,(⍎↓)
↑,∘⍎↓

┌─┼──┐
↑ , ┌┴┐
    ⍎ ↓

┌─┼─┐
↑ ∘ ↓
 ┌┴┐
 , ⍎

In other words, we made a derived function with jot: ,∘⍎. That turned out well: the tacit version is shorter than the explicit, and no less readable.

A few more?

This dfn takes a rational to the right and tries to compute a vector representing the corresponding fraction:

{(1∧⍵)÷1,⍵} 0.75

3 4

A fork, with both tines also being forks.

f1 ← {1∧⍵}
f2 ← {1,⍵}
{(f1 ⍵) ÷ f2 ⍵} 0.75

3 4

We can convert the tine forks directly by swapping ⍵ for ⊢ and {} for ():

((1∧⊢)÷1,⊢) 0.75

3 4

This one shifts a vector of numbers the specified number of steps to the left, padding with zeros on the right:

3 {⍺↓⍵,⍺↑0} ⍳10

3 4 5 6 7 8 9 0 0 0

Looks easy, right? Tempting to to jump to the conclusion that this is a fork on Catenate, f,g – it’s not.

The complication is the take at the end, which has an array right argument which isn’t allowed in a train: we need to Commute that one. So starting from the right, we have a dyadic function as ⍺↑0, preceded by ⍵,. So that’s our first fork of the form ⊢,f:

⊢,0↑⍨⊣

┌─┼───┐
⊢ , ┌─┼─┐
    0 ⍨ ⊣
    ┌─┘
    ↑

Before that we have ⍺↑ which together with what we already did also makes a fork, this time ⊣↑g:

⎕ ← shift ← ⊣↓⊢,0↑⍨⊣

┌─┼───┐
⊣ ↓ ┌─┼───┐
    ⊢ , ┌─┼─┐
        0 ⍨ ⊣
        ┌─┘
        ↑

3 shift ⍳10

3 4 5 6 7 8 9 0 0 0

Note that again it’s tempting to say that ⊣f⊢ is just f like we did earlier, but that makes the same slip as we started with – they don’t belong to one fork:

↓,0↑⍨⊣

┌─┼───┐
↓ , ┌─┼─┐
    0 ⍨ ⊣
    ┌─┘
    ↑

Shuffle the array

The LeetCode problem 1470 was posed as a chat mini challenge on APL Orchard to produce a tacit solution, and some elegant solutions were presented. Let’s look at that problem.

The task is to take a vector of length 2n, and essentially zip the first half with the second, and flatten:

Input: nums = [1,2,3,4,4,3,2,1], n = 4
Output: [1,4,2,3,3,2,4,1]

A dfn formulation is pretty straight-forward:

4 {,⍉2⍺⍴⍵} 1 2 3 4 4 3 2 1

1 4 2 3 3 2 4 1

which is reshape to 2 n, Transpose, Ravel – in fact, it’s kind of how we said it: “zip the first half with the second, and flatten”. However, that particular dfn doesn’t lend itself nicely to a tacit formulation. APL Orchard user @rak1507 proposed the following gem:

4 (∊↑,¨↓) 1 2 3 4 4 3 2 1

1 4 2 3 3 2 4 1

Remarkably clever, but kinda obvious (once you’ve seen it). This relies on Catenate each ,¨ as the (almost) “zip” instead of ,⍉:

1 2 3 4 ,¨ 4 3 2 1

┌→──┬───┬───┬───┐
│1 4│2 3│3 2│4 1│
└~─→┴~─→┴~─→┴~─→┘

The actual formulation is the tacit version of

4 {∊(⍺↑⍵),¨(⍺↓⍵)} 1 2 3 4 4 3 2 1

1 4 2 3 3 2 4 1

(∊↑,¨↓)

┌─┴─┐
∊ ┌─┼─┐
  ↑ ¨ ↓
  ┌─┘
  ,

Nice. But wait, there’s more. Adám’s version takes a wholly different approach, and do note the way the function takes its arguments, which is key to how this works:

(,∘⍉2@0⍴⊃) (1 2 3 4 4 3 2 1) 4

1 4 2 3 3 2 4 1

Not obvious how that works, right? Let’s look at the parse tree:

,∘⍉2@0⍴⊃

 ┌──┴──┐
 ∘   ┌─┼─┐
┌┴┐  @ ⍴ ⊃
, ⍉ ┌┴┐
    2 0

The interesting bit is the fork 2@0⍴⊃, so let’s look at that:

2@0⍴⊃

 ┌─┼─┐
 @ ⍴ ⊃
┌┴┐
2 0

(2@0⍴⊃) (1 2 3 4 4 3 2 1) 4

1 2 3 4
4 3 2 1

Aha. Yes, there’s the “fold in half” – but how does that work? The middle tine is clearly the reshape, and the right tine picks the first element, which makes sense, but what of the left tine?

2@0 ⊢ (1 2 3 4 4 3 2 1) 4

2 4

Wow. Did the penny drop? I think that qualifies as a code-golfer’s trick shot.

Other suggestions were:

((⍋≢⍴(⍳.5×≢))⊃¨⊂) 1 2 3 4 4 3 2 1 ⍝ Author: @Razetime -- no need for the length
(⊢⌷⍨∘⊂∘⍋∘⍋2|⍳∘≢)  1 2 3 4 4 3 2 1 ⍝ Author: @rak1507  -- no need for the length

1 4 2 3 3 2 4 1

1 4 2 3 3 2 4 1

Feel free to untangle those at your leisure.