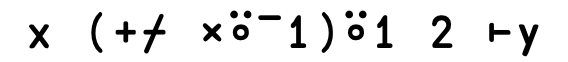Photo by Jonathan Singer on Unsplash

Indexing

Elegance is not a dispensable luxury but a factor that decides between success and failure. –Edsger Dijkstra

There are several ways of indexing into arrays and vectors. Some might even say “too many”. A good start point is to read up on indexing in Dyalog’s documentation, and Richard Park’s webinar on the topic is extremely helpful, too.

But as before, we begin by setting our index origin, extra important as we’re about to discuss indexing. Whilst we’re at it, let’s also ensure we have output boxing turned on.

⎕IO ← 0

]box on

Was ON

Anyway – back to indexing. Crucially, elements of vectors and matrices are always scalars, but a scalar can be an enclosed vector or matrix. Indexing with [] or ⌷ returns the box, not the element in the box. However, if the element is a simple scalar, it’s the same thing.

Let’s look at bracket indexing first.

Bracket indexing [ ]

Bracket indexing is similar to how C-like languages index into arrays:

⎕ ← v ← 9 2 6 3 5 8 7 4 0 1
v[5]    ⍝ Grab the cell at index 5

9 2 6 3 5 8 7 4 0 1

8

However, unlike C (and its ilk), the indexing expression can be a vector, or even a higher-rank array:

v[5 2]  ⍝ Grab the cells at indices 5 and 2

8 6

We can mutate the vector or array via a bracket index, too:

v[3] ← ¯1
v

9 2 6 ¯1 5 8 7 4 0 1

Of course, this being APL, this idea extends to any shape of array, either by separating the axes by semi-colon:

]DISPLAY m ← 3 3⍴4 1 6 5 2 9 7 8 3 ⍝ a 3×3 matrix
m[1;1]  ⍝ Row 1, col 1
m[1;]   ⍝ Row 1
m[;1]   ⍝ Col 1

┌→────┐
↓4 1 6│
│5 2 9│
│7 8 3│
└~────┘

2

5 2 9

1 2 8

or by supplying one or more enclosed vectors, each with shape equal to the rank of the array:

m[⊂1 1] ⍝ Centre

2

m[(0 0)(1 1)(2 2)] ⍝ Three points along the main diagonal

4 2 3

As indicated above, bracket indexing references cells, not the values enclosed in the cells. For numeric or character scalars, there is no difference, but the difference is clear for a nested array:

⎕ ← m ← 3 3⍴(1 2 3)(3 2 1)(4 5 6)(5 3 1)(5 6 8)(7 1 2)(4 3 9)(3 7 6)(4 5 1)

┌─────┬─────┬─────┐
│1 2 3│3 2 1│4 5 6│
├─────┼─────┼─────┤
│5 3 1│5 6 8│7 1 2│
├─────┼─────┼─────┤
│4 3 9│3 7 6│4 5 1│
└─────┴─────┴─────┘

]DISPLAY m[1;1] ⍝ Note the returned enclosure.

┌─────────┐
│ ┌→────┐ │
│ │5 6 8│ │
│ └~────┘ │
└∊────────┘

Functional indexing ⌷

Whilst bracket-style indexing feels immediately familiar for those of us coming from a different programming language tradition, it is somewhat frowned upon amongst APLers. One reason for this is that it doesn’t follow APL’s normal strict right-to-left evaluation order as the indexing expression always must be evaluated first. As a consequence, it just stands out a bit: it’s neither a monadic or dyadic function call. Another reason is that bracket indexing doesn’t work in tacit functions, a topic we’ll cover in a later chapter.

There is an alternative native indexing method: functional, or Squad indexing. Squad, “squashed quad”, is the glyph ⌷. It can be seen mnemonically as the two square indexing brackets pushed together. Squad fixes some of the issues surrounding the bracket indexing method above (but introduces some new ones, too). As Squad is a normal dyadic function, it behaves just like any other of APL’s dyadic functions:

⎕ ← m ← 3 3⍴(1 2 3)(3 2 1)(4 5 6)(5 3 1)(5 6 8)(7 1 2)(4 3 9)(3 7 6)(4 5 1)

┌─────┬─────┬─────┐
│1 2 3│3 2 1│4 5 6│
├─────┼─────┼─────┤
│5 3 1│5 6 8│7 1 2│
├─────┼─────┼─────┤
│4 3 9│3 7 6│4 5 1│
└─────┴─────┴─────┘

1⌷m       ⍝ Row 1

┌─────┬─────┬─────┐
│5 3 1│5 6 8│7 1 2│
└─────┴─────┴─────┘

1 1⌷m     ⍝ Cell 1 1

┌─────┐
│5 6 8│
└─────┘

(⊂1 2)⌷m  ⍝ Rows 1 and 2

┌─────┬─────┬─────┐
│5 3 1│5 6 8│7 1 2│
├─────┼─────┼─────┤
│4 3 9│3 7 6│4 5 1│
└─────┴─────┴─────┘

However, selecting cells from other axes than the first requires you to specify the axes explicitly with square brackets, which arguably looks a bit clumsy. Note that this isn’t a bracket index, even though it looks like one. For example, here’s how we select cell 2 from axis 1 (i.e. third column):

2⌷[1]m

┌─────┬─────┬─────┐
│4 5 6│7 1 2│4 5 1│
└─────┴─────┴─────┘

or we could avoid the bracketed axis specification by picking the row from the matrix’s Transpose, ⍉:

2⌷⍉m

┌─────┬─────┬─────┐
│4 5 6│7 1 2│4 5 1│
└─────┴─────┴─────┘

Squad index does not let you mutate the array.

Another issue with Squad is that it flips the conventions established by the bracket indexing method. Let’s return to a couple of our examples from the bracket indexing section, and compare those with how you’d achieve the same thing with Squad:

n ← 3 3⍴4 1 6 5 2 9 7 8 3

n[⊂1 1] ⍝ Centre

2

n[(0 0)(1 1)(2 2)] ⍝ Three points along the main diagonal

4 2 3

Squad’s indexing expression, unlike that of bracket indexing’s, specifies the coordinate for each axis in turn:

1 1⌷n ⍝ Centre

2

If we enclose the indexing expression we pick major cells, which arguably “feels” odd compared with how bracket indexing behaves:

(⊂1 1)⌷n ⍝ Repeat row 1

5 2 9
5 2 9

So, how do we choose the three diagonal cells with Squad? With great difficulty, as it turns out. For this we need Sane indexing, up next.

Sane indexing

Some APLers are unhappy with Squad’s semantics, and have proposed yet another mechanism, called Sane indexing or Select. It’s not yet built into Dyalog, but it can be defined as:

I←⌷⍨∘⊃⍨⍤0 99 ⍝ Sane indexing

For the purposes of this explanation, it matters less how that incantation hangs together (we’ll return to how this works in the section on the Rank operator, ⍤, later), but it does have a set of nice properties for the user.

Compare and contrast Squad and Sane indexing:

⎕ ← m ← 3 3⍴(1 2 3)(3 2 1)(4 5 6)(5 3 1)(5 6 8)(7 1 2)(4 3 9)(3 7 6)(4 5 1)

┌─────┬─────┬─────┐
│1 2 3│3 2 1│4 5 6│
├─────┼─────┼─────┤
│5 3 1│5 6 8│7 1 2│
├─────┼─────┼─────┤
│4 3 9│3 7 6│4 5 1│
└─────┴─────┴─────┘

Index with a vector:

1 2I m   ⍝ Sane:  select leading axis cells 1 and 2, or m[1 2;]
1 2⌷ m   ⍝ Squad: select m[⊂1 2]

┌─────┬─────┬─────┐
│5 3 1│5 6 8│7 1 2│
├─────┼─────┼─────┤
│4 3 9│3 7 6│4 5 1│
└─────┴─────┴─────┘

┌─────┐
│7 1 2│
└─────┘

Index with an enclosed vector:

(⊂1 2)I m  ⍝ Sane:  select m[⊂1 2]
(⊂1 2)⌷ m  ⍝ Squad: select m[1 2;]

┌─────┐
│7 1 2│
└─────┘

┌─────┬─────┬─────┐
│5 3 1│5 6 8│7 1 2│
├─────┼─────┼─────┤
│4 3 9│3 7 6│4 5 1│
└─────┴─────┴─────┘

So you can think of Sane indexing as Squad, but closer to the behaviour of the bracket indexing expression. We can finally select a bunch of cells by index:

(0 0)(1 2)(2 2)I m ⍝ Multiple cells by index, like m[(0 0)(1 2)(2 2)]

┌─────┬─────┬─────┐
│1 2 3│7 1 2│4 5 1│
└─────┴─────┴─────┘

Boolean indexing: compress

But wait! There’s more to APL indexing. In fact, much of APL’s expressive power comes from its central application of bit-Boolean arrays, and it’s typically highly optimised. It’s a concept you don’t often see in non-array languages, but you may have been exposed to limited forms of it from bolt-on array libraries such as Python’s NumPy. Similar functionality can be achieved using a filter function taking a predicate in other languages.

The core idea is actually quite simple: select cells from an array by using a Boolean array as the indexing method, where a 1 means “yes, this one” and a 0 means “nope, not this one”. We use Compress to do this in APL, one of the several things represented by a forward slash /.

data   ← 0 1 2 3 4 5 6 7 8 9
select ← 0 0 1 0 1 1 0 1 1 0 ⍝ Select elements 2, 4, 5, 7 and 8
select/data

2 4 5 7 8

Compress is really a special case of the Replicate function, where the left argument is a Boolean vector. However, we can view the left argument more generally as a specification of how many times we should pick each element. In the compression case, that’s either 1 or 0. In the more general case we need not constrain ourselves to binary – we can pick any number:

select ← 1 3 0 0 5 0 7 0 0 1
select/data

0 1 1 1 4 4 4 4 4 6 6 6 6 6 6 6 9

Replicate and Compress apply along the given axis in higher-rank arrays, either via Replicate first (⌿) or by specifiying the axis explicitly with the bracket axis notation, /[axis]:

m ← 3 3⍴9?9
]DISPLAY m

┌→────┐
↓3 0 5│
│4 1 8│
│6 7 2│
└~────┘

select ← 0 1 0

select⌿m ⍝ Replicate first

4 1 8

select/m ⍝ Replicate

0
1
7

Pick ⊃

Yet another way to index into arrays is to use Pick. Pick eh… picks elements, not boxes, which often comes in handy. A monadic Pick picks the first element.

⎕ ← m ← 3 3⍴(1 2 3)(3 2 1)(4 5 6)(5 3 1)(5 6 8)(7 1 2)(4 3 9)(3 7 6)(4 5 1)

┌─────┬─────┬─────┐
│1 2 3│3 2 1│4 5 6│
├─────┼─────┼─────┤
│5 3 1│5 6 8│7 1 2│
├─────┼─────┼─────┤
│4 3 9│3 7 6│4 5 1│
└─────┴─────┴─────┘

Element at 1;1 - note, no box:

(⊂1 1)⊃m

5 6 8

First element - note, no box:

⊃m

1 2 3

Reach indexing

Reach indexing is how you access elements of nested arrays. Note that nested arrays carry with them performance penalties and are best avoided if at all possible.

⎕ ← G ← 2 3⍴('Adam' 1)('Bob' 2)('Carl' 3)('Danni' 4)('Eve' 5)('Frank' 6)
G[⊂(0 1)0] ⍝ First element of the vector nested at ⊂0 1 of G
G[((0 0)0)((1 2)1)]

┌─────────┬───────┬─────────┐
│┌────┬─┐ │┌───┬─┐│┌────┬─┐ │
││Adam│1│ ││Bob│2│││Carl│3│ │
│└────┴─┘ │└───┴─┘│└────┴─┘ │
├─────────┼───────┼─────────┤
│┌─────┬─┐│┌───┬─┐│┌─────┬─┐│
││Danni│4│││Eve│5│││Frank│6││
│└─────┴─┘│└───┴─┘│└─────┴─┘│
└─────────┴───────┴─────────┘

┌───┐
│Bob│
└───┘

┌────┬─┐
│Adam│6│
└────┴─┘

Assignable indexing expressions

As we saw above, bracket indexing is assignable, meaning that we can mutate the array. It is not the only assignable indexing expression in APL. The full list of selective assignment functions is available from the Dyalog documentation. It’s worth studying this manual page, as it unlocks quite a few crafty ways of getting data into arrays.

For example, we can change the diagonal of a matrix by assigning directly to a dyadic Transpose by noting that 0 0⍉m is the main diagonal of the matrix m:

]DISPLAY m ← 3 3⍴9?9
(0 0⍉m) ← ¯1 ¯1 ¯1 ⍝ 0 0⍉m is the main diagonal.
]DISPLAY m

┌→────┐
↓1 2 3│
│4 8 0│
│6 5 7│
└~────┘

┌→───────┐
↓¯1  2  3│
│ 4 ¯1  0│
│ 6  5 ¯1│
└~───────┘

Indeed, we can even assign via Boolean indexing expressions, which might not be immediately obvious:

data   ← 0 1 2 3 4 5 6 7 8 9
select ← 0 0 1 0 1 1 0 1 1 0

(select/data) ← ¯1 ¯1 ¯1 ¯1 ¯1
data

0 1 ¯1 3 ¯1 ¯1 6 ¯1 ¯1 9

Perhaps even less obvious is assigning to Take:

⎕ ← s ← 'This is a string'
(2↑s) ← '**'
s

This is a string

**is is a string

…or even Compress each:

s←'This' 'is' (,'a') 'string' 'without' 'is.'
((s='i')/¨s)←'*'
s

┌────┬──┬─┬──────┬───────┬───┐
│Th*s│*s│a│str*ng│w*thout│*s.│
└────┴──┴─┴──────┴───────┴───┘