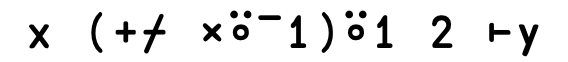Glyphiary

Are you quite sure that all those bells and whistles, all those wonderful facilities of your so called powerful programming languages, belong to the solution set rather than the problem set? –Edsger Dijkstra

Learning what each glyph does is an unavoidable chunk of time investment. However, there are some mnemonic cues sometimes based on where they sit on the keyboard, or that related functions sometimes have glyphs that are visually similar. Other times all bets are off: here’s looking at you, /…

We’re not going to cover them all. Learn them a few at a time as the need arises. Use the language bar in RIDE. But let’s run through some of the immediately handy ones.

But first, the usual dance:

⎕IO ← 0            ⍝ Index origin is zero
]box on -style=max ⍝ Show boxes at max verbosity
]rows on           ⍝ Don't wrap long output lines

┌→────────────────┐
│Was ON -style=max│
└─────────────────┘

┌→──────┐
│Was OFF│
└───────┘

Let’s have a random matrix for our demonstration purposes. We’ve met Shape (⍴) already, but we’ll get dyadic ? – called Deal – for free. It gives us a random selection of numbers from a set, without replacement:

⎕ ← mat ← 3 4⍴12?12 ⍝ Ladies and gentlemen: our matrix

┌→────────┐
↓3  0  5 1│
│7  9  8 6│
│2 10 11 4│
└~────────┘

Tally, Depth, Match: ≢≡

Tally, monadic ≢, gives the number of major cells in an array, kind of like Python’s len():

≢7 5 1 2 9
≢'Hello world'
≢mat

 
5

  
11

 
3

Pretty straight-forward. Monadic Equal underbar, ≡ is Depth – the max level of nesting:

≡1 2 3 4
≡(1 2)(3 4)
≡((1 2)(2 3))((4 5)(6 7))
≡(1 2)(3 4)3

 
1

 
2

 
3

  
¯2

The last case, giving ¯2, means that the max depth is 2, but that not all cells are at the same depth. Depth is not rank. Say it with me: depth is not rank, depth is not rank, depth is not rank…

Turning to the dyadic forms, ≡ is Match, and with a pleasing visual symmetry, ≢ is Not match. We can think of Match being “deep equals for arrays”: same rank, same order, same depth, every element the same:

1 2 3 4 ≡ 1 2 3 4 5
1 2 3 4 ≡ 1 2 3 4
1 2 3 4 ≡ 4 1 2 3
1 2 3 4 ≡ 1 4⍴1 2 3 4

 
0

 
1

 
0

 
0

Transpose, Reverse and Rotate: ⍉⊖⌽

Three glyphs used to change arrays around are Transpose (⍉), Reverse (⊖) and Rotate (⌽). They all look like a circle overstruck with a line. For example:

⍉mat ⍝ Transpose
⌽mat ⍝ Reverse
⊖mat ⍝ Reverse first

┌→─────┐
↓3 7  2│
│0 9 10│
│5 8 11│
│1 6  4│
└~─────┘

┌→────────┐
↓1  5  0 3│
│6  8  9 7│
│4 11 10 2│
└~────────┘

┌→────────┐
↓2 10 11 4│
│7  9  8 6│
│3  0  5 1│
└~────────┘

The two reverse glyphs mirror the issue we’ve seen with Replicate (/) vs Replicate first (⌿) – if you can, use the -first versions (the leading axis versions), and if you want to apply them along other axes, use either Rank ⍤ or the [axis] notation:

⊖⍤1⊢mat ⍝ Apply reverse-first to second axis using Rank
⊖[1]mat ⍝ Apply reverse-first to second axis bracket-axis

┌→────────┐
↓1  5  0 3│
│6  8  9 7│
│4 11 10 2│
└~────────┘

┌→────────┐
↓1  5  0 3│
│6  8  9 7│
│4 11 10 2│
└~────────┘

Both Transpose and Reverse can be applied dyadically, too, which presents us with a slight conundrum: the dyadic form of Transpose requires a deeper understanding of APL that we don’t yet have – we’ll push that one to its own chapter later on.

Dyadic ⊖ is actually Rotate first:

1 2 ¯1 0⊖mat

┌→────────┐
↓7 10 11 1│
│2  0  5 6│
│3  9  8 4│
└~────────┘

Here, the left argument vector specifies the per-column magnitude and direction of the rotation.

Mix, Split, Take and Drop: ↓↑

Mix ↑ raises the rank by 1. Easiest to visualise as a means of turning a nested vector into a matrix (but works for any rank):

⎕ ← v ← 'Hello' 'world'
↑v

┌→────────────────┐
│ ┌→────┐ ┌→────┐ │
│ │Hello│ │world│ │
│ └─────┘ └─────┘ │
└∊────────────────┘

┌→────┐
↓Hello│
│world│
└─────┘

Split ↓, unsurprisingly, goes the other way; reducing rank:

⎕ ← m ← 3 3⍴9?9
↓m

┌→────┐
↓8 0 3│
│6 5 2│
│7 1 4│
└~────┘

┌→────────────────────────┐
│ ┌→────┐ ┌→────┐ ┌→────┐ │
│ │8 0 3│ │6 5 2│ │7 1 4│ │
│ └~────┘ └~────┘ └~────┘ │
└∊────────────────────────┘

Mix and Split, when combined with Transpose, make for a bit of a power-combo, ↓⍉↑, occasionally dubbed Remix, or Zip:

⎕ ← v ← (0 6 3)(2 5 1)(4 7 8)
↓⍉↑v

┌→────────────────────────┐
│ ┌→────┐ ┌→────┐ ┌→────┐ │
│ │0 6 3│ │2 5 1│ │4 7 8│ │
│ └~────┘ └~────┘ └~────┘ │
└∊────────────────────────┘

┌→────────────────────────┐
│ ┌→────┐ ┌→────┐ ┌→────┐ │
│ │0 2 4│ │6 5 7│ │3 1 8│ │
│ └~────┘ └~────┘ └~────┘ │
└∊────────────────────────┘

Whilst it’s tempting to think of Remix as the zip() found in, for example, Python, note that it most likely behaves differently to what you’re used to:

↓⍉↑(1 2 3 4)(5 6)(7 8 9 10)

┌→─────────────────────────────────┐
│ ┌→────┐ ┌→────┐ ┌→────┐ ┌→─────┐ │
│ │1 5 7│ │2 6 8│ │3 0 9│ │4 0 10│ │
│ └~────┘ └~────┘ └~────┘ └~─────┘ │
└∊─────────────────────────────────┘

Python 3.9.0 (default, Nov 15 2020, 06:25:35) 
[Clang 10.0.0 ] :: Anaconda, Inc. on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> l = [[1,2,3,4],[5,6],[7,8,9,10]]
>>> list(zip(*l))
[(1, 5, 7), (2, 6, 8)]

APL abhors ragged arrays and will inject the “prototype” element for whatever the element type is to ensure that all cells are the same size – Python has no concept of array as such, and so abandons play if an element can’t be filled. Mixing a vector with cells of unequal numbers of elements in each cell will show us what happens:

↑(1 2 3 4)(5 6)(7 8 9 10)

┌→───────┐
↓1 2 3  4│
│5 6 0  0│
│7 8 9 10│
└~───────┘

Dyadically, Mix and Split become Take and Drop. Take … takes cells:

1↑(1 2 3 4)(5 6)(7 8 9 10) ⍝ Take 1
2↑(1 2 3 4)(5 6)(7 8 9 10) ⍝ Take 2

┌→──────────┐
│ ┌→──────┐ │
│ │1 2 3 4│ │
│ └~──────┘ │
└∊──────────┘

┌→────────────────┐
│ ┌→──────┐ ┌→──┐ │
│ │1 2 3 4│ │5 6│ │
│ └~──────┘ └~──┘ │
└∊────────────────┘

Note carefully the fact that Take returns cells, not elements, even if you take 1. Recalling the indexing chapter, Take 1 is equivalent to Squad 0, not Pick 0:

0⌷(1 2 3 4)(5 6)(7 8 9 10) ⍝ Squad 0 returns a cell
0⊃(1 2 3 4)(5 6)(7 8 9 10) ⍝ Pick 0 returns an element

┌───────────┐
│ ┌→──────┐ │
│ │1 2 3 4│ │
│ └~──────┘ │
└∊──────────┘

┌→──────┐
│1 2 3 4│
└~──────┘

We can also use negative numbers to take from the rear:

¯1↑(1 2 3 4)(5 6)(7 8 9 10) ⍝ Take 1 from the back

┌→───────────┐
│ ┌→───────┐ │
│ │7 8 9 10│ │
│ └~───────┘ │
└∊───────────┘

Drop does what we hopefully expect:

1↓(1 2 3 4)(5 6)(7 8 9 10)  ⍝ Drop 1 from the front
¯1↓(1 2 3 4)(5 6)(7 8 9 10) ⍝ Drop 1 from the back

┌→─────────────────┐
│ ┌→──┐ ┌→───────┐ │
│ │5 6│ │7 8 9 10│ │
│ └~──┘ └~───────┘ │
└∊─────────────────┘

┌→────────────────┐
│ ┌→──────┐ ┌→──┐ │
│ │1 2 3 4│ │5 6│ │
│ └~──────┘ └~──┘ │
└∊────────────────┘

Take and Drop work on any rank array:

mat
1↑mat ⍝ Take first cell
1↓mat ⍝ Drop first cell

┌→────────┐
↓3  0  5 1│
│7  9  8 6│
│2 10 11 4│
└~────────┘

┌→──────┐
↓3 0 5 1│
└~──────┘

┌→────────┐
↓7  9  8 6│
│2 10 11 4│
└~────────┘

Index generator and Index of: ⍳

Iota, ⍳, called Index generator (or Interval) when used monadically and Index of when used dyadically is one to figure out early. Note that there is another glyph that looks similar, iota underbar, ⍸, that does something entirely different, so don’t confuse the two!

The monadic case generates an integer interval, starting from the currently set ⎕IO (0 in our case, remember):

⍳10

┌→──────────────────┐
│0 1 2 3 4 5 6 7 8 9│
└~──────────────────┘

Thinking of this as a monadic function taking a shape vector, this generalises to more complex shapes:

⍳3 4

┌→────────────────────────┐
↓ ┌→──┐ ┌→──┐ ┌→──┐ ┌→──┐ │
│ │0 0│ │0 1│ │0 2│ │0 3│ │
│ └~──┘ └~──┘ └~──┘ └~──┘ │
│ ┌→──┐ ┌→──┐ ┌→──┐ ┌→──┐ │
│ │1 0│ │1 1│ │1 2│ │1 3│ │
│ └~──┘ └~──┘ └~──┘ └~──┘ │
│ ┌→──┐ ┌→──┐ ┌→──┐ ┌→──┐ │
│ │2 0│ │2 1│ │2 2│ │2 3│ │
│ └~──┘ └~──┘ └~──┘ └~──┘ │
└∊────────────────────────┘

In other words, iota generates all possible indices into an array with the shape of its argument.

In the dyadic form, iota becomes Index of, another useful thing to know. Index of tells us the index of the first occurrence of an element:

'Hello world'⍳'o'

 
4

The right argument can have any shape, but the left argument is usually a vector.

'Hello world'⍳'od'

┌→───┐
│4 10│
└~───┘

A nifty feature is that if the right element isn’t found, the returned index is ⎕IO+≢⍺ – the index origin (which in our case is 0) plus the length of the left argument. This can be used to provide a default match for items not found:

⎕ ← staff ← 'Adam' 'Bob' 'Charlotte'
lookup ← staff,⊂'Not found'
lookup[staff⍳'Bob' 'David']

┌→─────────────────────────┐
│ ┌→───┐ ┌→──┐ ┌→────────┐ │
│ │Adam│ │Bob│ │Charlotte│ │
│ └────┘ └───┘ └─────────┘ │
└∊─────────────────────────┘

┌→──────────────────┐
│ ┌→──┐ ┌→────────┐ │
│ │Bob│ │Not found│ │
│ └───┘ └─────────┘ │
└∊──────────────────┘

Where, Interval Index: ⍸

Iota-underbar, ⍸, is Where as a monad, and Interval Index as a dyad.

Where gives the indices of an array where the value is non-zero. For example,

⍸1 0 0 1 0 1 0 1 1 1 0 1 0 1

┌→────────────────┐
│0 3 5 7 8 9 11 13│
└~────────────────┘

This can be combined with indexing to select a subset that matches some criterion:

⎕←nums←⍳20
nums[⍸0=5|nums] ⍝ Find all numbers divisible by 5

┌→────────────────────────────────────────────────┐
│0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19│
└~────────────────────────────────────────────────┘

┌→────────┐
│0 5 10 15│
└~────────┘

It works for any rank, of course:

3 3⍴1 0 0 1 1 0 0 1 0
⍸3 3⍴1 0 0 1 1 0 0 1 0

┌→────┐
↓1 0 0│
│1 1 0│
│0 1 0│
└~────┘

┌→────────────────────────┐
│ ┌→──┐ ┌→──┐ ┌→──┐ ┌→──┐ │
│ │0 0│ │1 0│ │1 1│ │2 1│ │
│ └~──┘ └~──┘ └~──┘ └~──┘ │
└∊────────────────────────┘

You probably expected that. Perhaps more surprising is that the right argument array does not have to be Boolean:

⍸0 1 0 2 0 3 0 4 0 5

┌→────────────────────────────┐
│1 3 3 5 5 5 7 7 7 7 9 9 9 9 9│
└~────────────────────────────┘

It still finds the indices of non-zero elements, but this time it uses the element itself as the repeat count. In the result in example above, we have a single 1, as the right argument array has a 1 at index 1. We have four 7s, as the array has a 4 in index 7.

When used dyadically, we have interval index. Interval index is a binning algorithm – given a set of ranged bins in order, it picks the bin corresponding to the arguments. Here’s how it works:

1 3 5 7 9⍸8 9 0  ⍝ bin 8, 9 and 0 over the intervals 1 3 5 7 9

┌→─────┐
│3 4 ¯1│
└~─────┘

Consider the gaps between the elements to the left. The first interval is then [1, 3), the second is [3, 5), the third is [5, 7) etc. An element belongs to the bin where it is greater than or equal to the lower end, and less than the upper end.

1 3 5 7 9⍸5      ⍝ elements on on boundary goes in the higher bin

 
2

As we saw above, elements smaller than the first bin gets a bin number one less than the index origin (in our case the index origin is 0 so our “low bin” is ¯1), which is assumed to cover every number lower than the first bin. Similarly, elements greater than the last bin will end up with a bin number equal to the index of the last element to the left:

3 5 7 9⍸0 100

┌→───┐
│¯1 3│
└~───┘

It works for other types, too:

'AEIOU'⍸'HELLO WORLD'

┌→─────────────────────┐
│1 1 2 2 3 ¯1 4 3 3 2 0│
└~─────────────────────┘

In other words, “H” comes on or after “E” but not after “I”, “E” is on or after “E” etc.

Typical use cases for bin search involves various kinds of classification. For example, in the UK, alcoholic beverages are taxed based on their alcohol by volume (abv) percentage. Let’s consider cider and perry:

Class or description	Tax type code	Rate of excise duty/hl
abv does not exceed 1.2%	431	£0
abv exceeding 1.2% but less than 6.9%	481	£40.38
abv at least 6.9% but not exceeding 7.5%	487	£50.71
abv at least 7.5% but not exceeding 8.5%	483	£61.04

Given the following ciders with the associated abv, what are their respective tax code and tax rate per hecto-litre?

ciders←'Kopparberg Sparkling Rose' 'Bulmers Original' 'Crispin the Jacket' 'Old Mout Cherries & Berries'
abv←7.0 4.5 8.3 0.0

Let’s encode the table above into a set of vectors first:

code←431 481 487 486
rate←0 40.38 50.71 61.04
limits←1.2 6.9 7.5 8.5

Let’s find the bins from the limits, and add one to capture the -1 bin appropriately:

⎕←bin←1+limits⍸abv

┌→──────┐
│2 1 3 0│
└~──────┘

Now we can lay this out nicely,

⍕('Name' 'Rate' 'Code')⍪⍉↑(ciders (rate[bin]) (code[bin]))

┌→─────────────────────────────────────────┐
↓ Name                          Rate  Code │
│ Kopparberg Sparkling Rose    50.71   487 │
│ Bulmers Original             40.38   481 │
│ Crispin the Jacket           61.04   486 │
│ Old Mout Cherries & Berries   0      431 │
└──────────────────────────────────────────┘

Ravel, Catenate, Enlist, Member: ,⍪∊

Ravel, monadic , and Enlist, monadic ∊, do related things: Ravel creates a vector of the major cells of its argument, and Enlist creates a vector of the elements of its argument. For non-nested arrays, there is no difference:

simple ← 3 4⍴3 0 5 1 7 9 8 6 2 10 11 4
,simple ⍝ Ravel
∊simple ⍝ Enlist

┌→────────────────────────┐
│3 0 5 1 7 9 8 6 2 10 11 4│
└~────────────────────────┘

┌→────────────────────────┐
│3 0 5 1 7 9 8 6 2 10 11 4│
└~────────────────────────┘

For a nested array, the difference is clearer:

⎕ ← nested ← ↑((2 3)(4 5))((6 7)(8 9))
,nested ⍝ Ravel
∊nested ⍝ Enlist

┌→────────────┐
↓ ┌→──┐ ┌→──┐ │
│ │2 3│ │4 5│ │
│ └~──┘ └~──┘ │
│ ┌→──┐ ┌→──┐ │
│ │6 7│ │8 9│ │
│ └~──┘ └~──┘ │
└∊────────────┘

┌→────────────────────────┐
│ ┌→──┐ ┌→──┐ ┌→──┐ ┌→──┐ │
│ │2 3│ │4 5│ │6 7│ │8 9│ │
│ └~──┘ └~──┘ └~──┘ └~──┘ │
└∊────────────────────────┘

┌→──────────────┐
│2 3 4 5 6 7 8 9│
└~──────────────┘

In their dyadic guises, , becomes Catenate, and ∊ becomes Membership.

Catenate merges its left and right arguments:

1 2 3 4 , 5 6 'hello'
1 2 3 4 5 6 , 'hello'

┌→────────────────────┐
│             ┌→────┐ │
│ 1 2 3 4 5 6 │hello│ │
│             └─────┘ │
└∊────────────────────┘

┌→────────────────┐
│1 2 3 4 5 6 hello│
└+────────────────┘

The distinction above is perhaps not obvious - and without ]box on they would look identical. In the first case, Catenate’s right argument is a nested vector, whereas in the second case, it’s a simple character vector.

Note that Catenate is trailling axis. There is a leading axis version, too, ⍪, called Laminate – or, perhaps more logically – Catenate first.

We can catenate higher-rank arrays, too:

(3 3⍴⍳9),(3 3⍴⍳9) ⍝ Catenate-last (new cols)
(3 3⍴⍳9)⍪(3 3⍴⍳9) ⍝ Catenate-first/laminate (new rows)

┌→──────────┐
↓0 1 2 0 1 2│
│3 4 5 3 4 5│
│6 7 8 6 7 8│
└~──────────┘

┌→────┐
↓0 1 2│
│3 4 5│
│6 7 8│
│0 1 2│
│3 4 5│
│6 7 8│
└~────┘

Dyadic ∊ is Membership, another handy glyph in your arsenal:

'l'∊'Hello world'

 
1

It’s not unlike Python’s in:

>>> 'l' in 'Hello world'
True

at least at a superficial level. The APL version extends naturally to higher-rank arrays:

'lo w'∊'Hello world'

┌→──────┐
│1 1 1 1│
└~──────┘

whereas Python would see that as is substring:

>>> 'lo w' in 'Hello world'
True

You can, of course, get a similar substring behaviour in APL, too, but you need a different approach:

'lo'(⍸⍷)'Hello world' ⍝ Index of start of substring

┌→┐
│3│
└~┘

but we need a bit more flesh on our APL bones before we’re ready for that – see the Finding things section later!

Selfie, Commute, Constant: ⍨

A firm favourite, the Selfie (although it’s really called Commute), mirroring the confused look of the APL neophyte: ⍨. A monadic operator, the selfie commutes the left and right arguments of its operand function. At first, this seems beyond pointless – worse, in fact: it seems to offer nothing but added, deliberate obfuscation:

⎕ ← v ← 6 9 5 2 0 9
v↑⍨1     ⍝ Take 1 but commute arguments ⍨

┌→──────────┐
│6 9 5 2 0 9│
└~──────────┘

┌→┐
│6│
└~┘

As it turns out, it has its legitimate uses. Consider the consequences of APL’s right to left evaluation order. If you have a dyadic function application with a complex expression to the left, you’re forced to introduce parenthesis to ensure that the left side is fully evaluated before it is passed to the function. The commute operator, by shifting the complex expression to the right side, avoids this.

Compare the following two equivalent forms (disregarding for the moment what they mean):

{⍵⊂⍨1,2≠/⍵}
{(1,2≠/⍵)⊂⍵}

{⍵⊂⍨1,2≠/⍵}

{(1,2≠/⍵)⊂⍵}

So you could say “big deal, one glyph fewer to type”, and you’d have a point. But the main advantage is that, by commuting, we preserve the right-to-left evaluation order. By having parenthesised part of the expression, we have an unnatural evaluation order. With a few well-placed selfies we can read the expression as Ken intended.

As with anything, there’s a balance to be struck here. For the learner, selfies do make expressions harder, not easier, to read. The process of “flipping selfied expressions” occasionally helps when trying to deconstruct something someone else wrote.

If we give no left argument to the dyadic function derived by Selfie we echo the right argument to its left:

=⍨1 2 3 4 5

┌→────────┐
│1 1 1 1 1│
└~────────┘

which is the same as saying:

1 2 3 4 5 = 1 2 3 4 5

┌→────────┐
│1 1 1 1 1│
└~────────┘

If APL didn’t already have a Tally function built in (≢) we could make one as the sum-reduction of self-equals to count the number of elements in a vector, say:

tally ← +/=⍨

tally 1 2 3 4 5

 
5

If Selfie is given an array operand, it becomes Constant: it always returns its operand:

1⍨ 2
3 (1⍨) 2
1⍨ 2 3 4 5
1⍨¨ 2 3 4 5

 
1

 
1

 
1

┌→──────┐
│1 1 1 1│
└~──────┘

You can be excused for thinking that this is pretty pointless, but you’d be surprised how handy it can be. For example, you often find yourself wanting to create a vector of all the same value matching the shape of some other array:

⎕ ← m ← 3 3⍴9?9 
5⍨¨m ⍝ Make an array that looks like m, but will all elements 5

┌→────┐
↓0 6 3│
│2 5 1│
│4 7 8│
└~────┘

┌→────┐
↓5 5 5│
│5 5 5│
│5 5 5│
└~────┘

There are many other ways we could achieve the same thing, for example

5⍴⍨⍴m

┌→────┐
↓5 5 5│
│5 5 5│
│5 5 5│
└~────┘

but if you pronounce 5⍨¨m as “constant 5 for each element in m” it matches the problem description nicely.

Unique, Union, Intersection, Without: ∪∩~

We have the full complement of set operations at our disposal. Starting with Unique, monadic ∪, it does exactly what it says on the tin:

∪1 1 2 2 3 3 4 4 5 5 6 6
∪'hello world'

┌→──────────┐
│1 2 3 4 5 6│
└~──────────┘

┌→───────┐
│helo wrd│
└────────┘

In its dyadic version, ∪ becomes Union:

1 1 2 3 4 ∪ 1 2 5 6

┌→────────────┐
│1 1 2 3 4 5 6│
└~────────────┘

Note that the arguments aren’t proper sets. The above says “take ALL elements in the left argument, and add any element from the right which isn’t already present”.

Intersection, dyadic ∩, works similarly:

1 1 2 3 4 ∩ 1 2 5 6

┌→────┐
│1 1 2│
└~────┘

For each element to the left, keep it if it’s also in the right.

Dyadic ~ is Without – set difference:

1 1 2 3 4 5 ~ 1 3 5

┌→──┐
│2 4│
└~──┘

The monadic ~ is Boolean Not:

~1 0 1 1 0 0 1

┌→────────────┐
│0 1 0 0 1 1 0│
└~────────────┘

Grade up/down: ⍋⍒

To me, it’s a Christmas tree and a carrot, but these twins are called Grade up (⍋) and Grade down (⍒). They are APL’s very clever mechanisms for ordering arrays. To sort an array, we do:

⎕ ← data ← 110 109 204 40 105 201 2 208 160 143 213 31 21 317 132 242 164 176 67 18 75 89 18 7 20
data[⍋data]

┌→─────────────────────────────────────────────────────────────────────────────────────┐
│110 109 204 40 105 201 2 208 160 143 213 31 21 317 132 242 164 176 67 18 75 89 18 7 20│
└~─────────────────────────────────────────────────────────────────────────────────────┘

┌→─────────────────────────────────────────────────────────────────────────────────────┐
│2 7 18 18 20 21 31 40 67 75 89 105 109 110 132 143 160 164 176 201 204 208 213 242 317│
└~─────────────────────────────────────────────────────────────────────────────────────┘

So what does the Grade-up actually do? Let’s have a look:

⍋data

┌→───────────────────────────────────────────────────────────────┐
│6 23 19 22 24 12 11 3 18 20 21 4 1 0 14 9 8 16 17 5 2 7 10 15 13│
└~───────────────────────────────────────────────────────────────┘

Grading an array (up or down) produces a set of indices, not values. Consider the first element in the grade array. It says: the smallest element is to be found at index 6. The second-smallest is at index 23. The third smallest at index 19 etc.

At first blush, this seems like a roundabout way to sort something. First generate an indexing expression, then select elements according to this indexing expression. However, doing it this way – separating the determining of the order from the reordering of elements – has a number of advantages, chiefly that we can as easily apply the ordering to another array, not just the one that we generated the ordering from.

In any sort of data processing or analysis, this crops up all the time: give the customer names, ordered by contract date. Sort the keys based on the values. That sort of thing. You can also answer questions such as where is the smallest value?

⎕ ← minidx ← ⊃⍋data ⍝ Index of smallest value: first element of Grade-up
data[minidx]

 
6

 
2