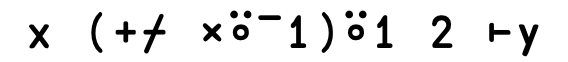The Key operator: `⌸`#

Overemphasis of efficiency leads to an unfortunate circularity in design: for reasons of efficiency early programming languages reflected the characteristics of the early computers, and each generation of computers reflects the needs of the programming languages of the preceding generation. –Kenneth E. Iverson

⎕IO ← 0
]box on
]rows on

Was ON

Was OFF

The monadic operator Key (⌸) groups things. It can, for example, be used to generate histograms, or if you are so inclined, you can think of it as similar to SQL’s GROUP BY clause.

Other resources on Key:

Dyalog docs
APL Orchard cultivation (also covering Stencil)

The function derived by Key is ambivalent (can be called either monadically or dyadically). The operand function can be any dyadic function returning a value.

Let’s look at the derived function, when called monadically:

{⍺⍵}⌸ 'bill' 'bob' 'bill' 'eric' 'bill' 'bob' 'eric' 'sue'

┌──────┬─────┐
│┌────┐│0 2 4│
││bill││     │
│└────┘│     │
├──────┼─────┤
│┌───┐ │1 5  │
││bob│ │     │
│└───┘ │     │
├──────┼─────┤
│┌────┐│3 6  │
││eric││     │
│└────┘│     │
├──────┼─────┤
│┌───┐ │7    │
││sue│ │     │
│└───┘ │     │
└──────┴─────┘

In this case, the operator function is called with each unique element from the argument array in turn as the left argument, and a vector of indices where they occur. If we wanted this to be a histogram, all we need to to is:

{⍺ (≢⍵)}⌸ 'bill' 'bob' 'bill' 'eric' 'bill' 'bob' 'eric' 'sue'

┌──────┬─┐
│┌────┐│3│
││bill││ │
│└────┘│ │
├──────┼─┤
│┌───┐ │2│
││bob│ │ │
│└───┘ │ │
├──────┼─┤
│┌────┐│2│
││eric││ │
│└────┘│ │
├──────┼─┤
│┌───┐ │1│
││sue│ │ │
│└───┘ │ │
└──────┴─┘

In the dyadic form, Key takes each unique element to the left, and groups the corresponding elements from the right. In other words, the following two formulations do the same thing:

names ← 'bill' 'bob' 'bill' 'eric' 'bill' 'bob' 'eric' 'sue'
{⍺⍵}⌸ names
names {⍺⍵}⌸ ⍳≢names

┌──────┬─────┐
│┌────┐│0 2 4│
││bill││     │
│└────┘│     │
├──────┼─────┤
│┌───┐ │1 5  │
││bob│ │     │
│└───┘ │     │
├──────┼─────┤
│┌────┐│3 6  │
││eric││     │
│└────┘│     │
├──────┼─────┤
│┌───┐ │7    │
││sue│ │     │
│└───┘ │     │
└──────┴─────┘

┌──────┬─────┐
│┌────┐│0 2 4│
││bill││     │
│└────┘│     │
├──────┼─────┤
│┌───┐ │1 5  │
││bob│ │     │
│└───┘ │     │
├──────┼─────┤
│┌────┐│3 6  │
││eric││     │
│└────┘│     │
├──────┼─────┤
│┌───┐ │7    │
││sue│ │     │
│└───┘ │     │
└──────┴─────┘

Let’s look at a slightly more involved example. Here are the Rugby Union Gallagher English Premiership results for Jan, 2021, home fixtures only. The 0-0 games were COVID cancellations.

results ← 'London Irish,31-22' 'Wasps,17-49' 'Gloucester,26-31' 'Worcester Warriors,17-21' 'Bristol,48-3' 'Leicester Tigers,15-25' 'Harlequins,27-27' 'Newcastle Falcons,22-10' 'Exeter Chiefs,7-20' 'Northampton Saints,0-0' 'Bath,44-52' 'Sale,20-13' 'London Irish,0-0' 'Leicester Tigers,36-31' 'Wasps,34-5' 'Gloucester,19-22' 'Bristol,29-17' 'Worcester Warriors,0-0'

We’ll do some quick and dirty slicing and dicing to separate team names from results.

table ← ⎕CSV ('-'⎕R','⊢results)''4
teams ← ⊣/table
scores ← table[;1 2]

which gives us

3 6⍴teams

┌────────────┬─────────────────┬─────────────┬──────────────────┬───────┬──────────────────┐
│London Irish│Wasps            │Gloucester   │Worcester Warriors│Bristol│Leicester Tigers  │
├────────────┼─────────────────┼─────────────┼──────────────────┼───────┼──────────────────┤
│Harlequins  │Newcastle Falcons│Exeter Chiefs│Northampton Saints│Bath   │Sale              │
├────────────┼─────────────────┼─────────────┼──────────────────┼───────┼──────────────────┤
│London Irish│Leicester Tigers │Wasps        │Gloucester        │Bristol│Worcester Warriors│
└────────────┴─────────────────┴─────────────┴──────────────────┴───────┴──────────────────┘

and

3 6⍴↓scores

┌─────┬─────┬─────┬─────┬─────┬─────┐
│31 22│17 49│26 31│17 21│48 3 │15 25│
├─────┼─────┼─────┼─────┼─────┼─────┤
│27 27│22 10│7 20 │0 0  │44 52│20 13│
├─────┼─────┼─────┼─────┼─────┼─────┤
│0 0  │36 31│34 5 │19 22│29 17│0 0  │
└─────┴─────┴─────┴─────┴─────┴─────┘

To illustrate the similarity with SQL’s GROUP BY, by using dyadic Key, we can group the scores under each team:

teams {⍺⍵}⌸ scores

┌────────────────────┬─────┐
│┌────────────┐      │31 22│
││London Irish│      │ 0  0│
│└────────────┘      │     │
├────────────────────┼─────┤
│┌─────┐             │17 49│
││Wasps│             │34  5│
│└─────┘             │     │
├────────────────────┼─────┤
│┌──────────┐        │26 31│
││Gloucester│        │19 22│
│└──────────┘        │     │
├────────────────────┼─────┤
│┌──────────────────┐│17 21│
││Worcester Warriors││ 0  0│
│└──────────────────┘│     │
├────────────────────┼─────┤
│┌───────┐           │48  3│
││Bristol│           │29 17│
│└───────┘           │     │
├────────────────────┼─────┤
│┌────────────────┐  │15 25│
││Leicester Tigers│  │36 31│
│└────────────────┘  │     │
├────────────────────┼─────┤
│┌──────────┐        │27 27│
││Harlequins│        │     │
│└──────────┘        │     │
├────────────────────┼─────┤
│┌─────────────────┐ │22 10│
││Newcastle Falcons│ │     │
│└─────────────────┘ │     │
├────────────────────┼─────┤
│┌─────────────┐     │7 20 │
││Exeter Chiefs│     │     │
│└─────────────┘     │     │
├────────────────────┼─────┤
│┌──────────────────┐│0 0  │
││Northampton Saints││     │
│└──────────────────┘│     │
├────────────────────┼─────┤
│┌────┐              │44 52│
││Bath│              │     │
│└────┘              │     │
├────────────────────┼─────┤
│┌────┐              │20 13│
││Sale│              │     │
│└────┘              │     │
└────────────────────┴─────┘

One more example. Given a vector, return the most frequent element, or if there are several, return all of those:

{⍵⌷⍨⊂0~⍨⊢/0,⊢⌸⍵} 'Mississippi' ⍝ Most frequent from APLCart

is

Ouch.

A lot of stuff there we haven’t seen yet, and rather ‘golfy’. Let’s unpick it, and see how far we get. From the right we first have our Key:

⊢⌸ 'Mississippi'

That’s just the indices of each unique element in turn, as if we’d written

{⍵}⌸ 'Mississippi'

We then prepend a 0 column

0,⊢⌸ 'Mississippi'

Why is this? It doesn’t seem to be necessary?

{⍵⌷⍨⊂0~⍨⊢/⊢⌸⍵} 'Mississippi'

is

This is just guarding against a special case – should the function be passed an empty argument, we don’t want to error:

{⍵⌷⍨⊂0~⍨⊢/⊢⌸⍵} '' ⍝ Note: DOMAIN ERROR

DOMAIN ERROR
      {⍵⌷⍨⊂0~⍨⊢/⊢⌸⍵}'' ⍝ Note: DOMAIN ERROR
              ∧

whereas with the prepended zeros it does the right thing:

{⍵⌷⍨⊂0~⍨⊢/0,⊢⌸⍵} ''

Anyway. After prepending a zero-col, we pick the last column:

⊢/0,⊢⌸ 'Mississippi'

0 10 6 0

This is how we can find the most frequent element(s) without any sorting – the vector(s) of indices of the most frequent elements will be the longest, and hence the non-zero elements in the last column will be corresponding to the last occurrence of the most frequent elements. We need to exclude the zeros first:

0~⍨⊢/⊢⌸ 'Mississippi'

10 6

and then enclose and index:

{⍵⌷⍨⊂0~⍨⊢/0,⊢⌸⍵} 'Mississippi'

is

Pretty cool, eh? But there is one gotcha here –

{⍵⌷⍨⊂0~⍨⊢/0,⊢⌸⍵}'abc'

bc

If the argument array contains only unique cells, we get the wrong result if we run under ⎕IO←0. Set it to 1 and it works:

{⎕IO←1⋄⍵⌷⍨⊂0~⍨⊢/0,⊢⌸⍵}'abc'

abc

This is, of course, to do with the excluding of zeros from the last column. Unfortunately, as we rely on 0 being the fill item for the array, so sadly we can’t prepend, say, a negative number instead of 0 for ⎕IO-independence:

{⍵⌷⍨⊂¯1~⍨⊢/¯1,⊢⌸⍵}'abc' ⍝ Whilst this works....
{⍵⌷⍨⊂¯1~⍨⊢/¯1,⊢⌸⍵}'Mississippi' ⍝ This breaks!

abc

MisM

Here are some drills on Key, suggested by Roger Hui in his APL Exercises. Try to work out in your head what the answers are before you reveal:

x ← 'Supercalifragilisticexpialidocious'

{⍺⍵}⌸x
{⍺ (≢⍵)}⌸x
{≢⍵}⌸x
{⍺}⌸x

┌─┬───────────────────┐
│S│0                  │
├─┼───────────────────┤
│u│1 32               │
├─┼───────────────────┤
│p│2 22               │
├─┼───────────────────┤
│e│3 20               │
├─┼───────────────────┤
│r│4 10               │
├─┼───────────────────┤
│c│5 19 29            │
├─┼───────────────────┤
│a│6 11 24            │
├─┼───────────────────┤
│l│7 14 25            │
├─┼───────────────────┤
│i│8 13 15 18 23 26 30│
├─┼───────────────────┤
│f│9                  │
├─┼───────────────────┤
│g│12                 │
├─┼───────────────────┤
│s│16 33              │
├─┼───────────────────┤
│t│17                 │
├─┼───────────────────┤
│x│21                 │
├─┼───────────────────┤
│d│27                 │
├─┼───────────────────┤
│o│28 31              │
└─┴───────────────────┘

S 1
u 2
p 2
e 2
r 2
c 3
a 3
l 3
i 7
f 1
g 1
s 2
t 1
x 1
d 1
o 2

1 2 2 2 2 3 3 3 7 1 1 2 1 1 1 2

Supercalifgstxdo

x ← 'abcdefghijk'
y ← 10+11 2⍴⍳22

x{⍺⍵}⌸y
x{⍺ (≢⍵)}⌸y
x{≢⍵}⌸y
x{⍺}⌸y
x{⍺(+/,⍵)}⌸y
x{⍺(⌈/,⍵)}⌸y
x{⍺(⌊/,⍵)}⌸y

┌─┬─────┐
│a│10 11│
├─┼─────┤
│b│12 13│
├─┼─────┤
│c│14 15│
├─┼─────┤
│d│16 17│
├─┼─────┤
│e│18 19│
├─┼─────┤
│f│20 21│
├─┼─────┤
│g│22 23│
├─┼─────┤
│h│24 25│
├─┼─────┤
│i│26 27│
├─┼─────┤
│j│28 29│
├─┼─────┤
│k│30 31│
└─┴─────┘

a 1
b 1
c 1
d 1
e 1
f 1
g 1
h 1
i 1
j 1
k 1

1 1 1 1 1 1 1 1 1 1 1

abcdefghijk

a 21
b 25
c 29
d 33
e 37
f 41
g 45
h 49
i 53
j 57
k 61

a 11
b 13
c 15
d 17
e 19
f 21
g 23
h 25
i 27
j 29
k 31

a 10
b 12
c 14
d 16
e 18
f 20
g 22
h 24
i 26
j 28
k 30

Learning APL

The Key operator: ⌸

The Key operator: `⌸`#

Learning APL

The Key operator: ⌸

The Key operator: ⌸#

The Key operator: `⌸`#