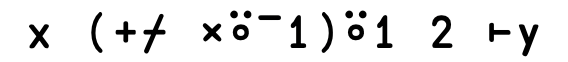The Rank/Atop operator: ⍤
Contents
The Rank/Atop operator: ⍤#
An algorithm must be seen to be believed. –Don Knuth
The somewhat startled-looking Rank operator, ⍤, has a reputation for being one of the harder ones to grasp. It sits on the ‘J’ key, a handy mnemonic, as it was an invention borrowed from the J-language. Well, it makes sense to me.
If ⍤ is given a right operand function it becomes Atop. We’ll talk about that after we’ve covered the Rank version.
Other resources on Rank and Atop:
Webinars: Rank Operator, Advanced Rank, Rank and Dyadic Transpose
APL Orchard cultivations: Basic Rank, Advanced Rank, Atop and Over
⎕IO ← 0
]box on
]rows on
In essence, the simple use of Rank drills into the argument array and applies its operand to sub-cells of a specified rank only.
Consider the following rank 3 array:
]DISPLAY m ← 3 3 3⍴27?27
≢⍴m
Let’s say we want to drop the first row of each layer of this array. In this case, we could use a bracket-axis specification to drop:
1↓[1]m ⍝ Apply drop ↓ to axis 1, i.e. the y-axis, with ⎕IO←0
However, this is now ⎕IO dependent, and the bracket-axis spec has some other undesirable properties, including the fact that it cannot be applied to user-defined functions.
The Rank operator allows us to solve this in a different way:
1↓⍤2⊢m
You can think of Rank in this case being closer to the problem statement: drop the first major cell of each sub-cell that has a rank one less than the argument. Or: in our 3D array, apply the drop to each of its constituent 2D arrays.
Note that Rank doesn’t equal depth, and this is part of the reason why the Rank operator can be confusing. So given a complex vector that contains a variety of scalars and higher-rank arrays, you can’t use the Rank operator to selectively apply a function to, say, just the vectors.
⎕ ← V ← (1 2 3)(2 2⍴1 1 1 1)(1)
≢⍤1⊢V ⍝ NOTE: this is wrong!
In this case, V is of course already a rank 1 array (i.e. a vector). But wait, there is more confusion to be had! The right operand doesn’t even have to be a scalar at all.
We already saw that if the right operand of ⍤ is a scalar, we are specifying which rank sub cells we want a function to apply to. For dyadic usage, we instead specify which sub-cells of the left argument should be paired up with which sub-cells of the right argument. It takes a while to wrap your head around this.
Here’s an example:
1 2 3,⍤0 1 ⊢ 'hello'
This says that the left argument of the derived function should be paired at rank 0 (that is each element) with the right argument at rank 1 (that is the whole vector in this case). If this feels reminiscent of an outer product, you’re not wrong.
In other words, Rank pairs up the arguments of the function it derives. We can examine which elements would be paired up by using the following incantation in place of our function:
rankpairs ← ⊂⍤,⍥⊂
if you know what that means, you probably don’t need to read this tutorial. If not, don’t worry – treat it as a debug statement:
1 2 3 rankpairs⍤0 1 ⊢ 'hello'
In the section on array indexing earlier, we introduced the concept of Sane Indexing without any further explanation on how it was working. Here it is again, as a tacit function:
I←⌷⍨∘⊃⍨⍤0 99 ⍝ Sane indexing, a.k.a select
Now that we understand a bit about Rank, we can at least make a start in taking that apart. So we have a Rank 0 99 to the right, stating that we should combine the left argument at rank 0 (scalars) with the right argument at “rank 99”. Rank 99 means “full rank” (Dyalog has an actual max rank of 15, so we could have used any number greater than or equal to 15). So we should combine “each scalar” to the left with “the whole thing, at whatever rank it happens to be” to the right.
The actual indexing is done by the leading Squad (⌷). Let’s de-selfie the expression and make it a dfn. Although we haven’t covered tacit functions yet, we can have the interpreter help us out a bit to see how that expression actually parses:
]box on -trains=tree ⍝ Visualise tacit functions as a parse tree
⌷⍨∘⊃⍨⍤0 99
If we separate out the Rank expression, after a bit of head-scratching, we arrive at
sane←{(⊃⍺)⌷⍵}
3 sane 'abcdefg'
1 2 3 sane⍤0 99⊢'abcdefg'
Hopefully, we can now see a bit clearer how it works – we simply pass the disclosed left argument vector to Squad, and Rank does the appropriate combination of left and right: each left element, to the whole (full-rank) of the right.
Here’s another example. Given two integer arrays of the same shape, can we replicate (or compress) the rows of one from the other? We might be excused if we think that we can replicate-reduce, but this doesn’t work:
]DISPLAY A ← 3 4⍴2 1 1 1 1 2 1 1 1 1 2 1
]DISPLAY B ← 3 4⍴1 2 3 4 1 2 3 4 1 2 3 4
(note: all expressions in the next cell will generate syntax or rank errors)
A∘//B ⍝ Nope... SYNTAX ERROR
{A/⍵}/B ⍝ Nope... RANK ERROR
A∘{⍺/⍵}/B ⍝ Nope... SYNTAX ERROR
SYNTAX ERROR: The function does not take a left argument
A∘//B ⍝ Nope... SYNTAX ERROR
∧
RANK ERROR
{A/⍵}/B ⍝ Nope... RANK ERROR
∧
SYNTAX ERROR: The function does not take a left argument
A∘{⍺/⍵}/B ⍝ Nope... SYNTAX ERROR
∧
Instead, we need to reach for Rank:
A/⍤1⊢B
If we spell it out in plain words, perhaps the use of Rank suggests itself: combine each major cell on the left with the corresponding major cell on the right, and apply the dyadic function “replicate”. Every time you think “combine each major cell on the left…”, you should think Rank.
As we’ve seen elsewhere, APL has a somewhat unholy mix of leading and trailing axis operators, mainly for historical reasons. Rank allows us to stick to the leading axis versions [Kromberg and Hui]:
Leading axis |
Trailling axis |
Operation |
|---|---|---|
(⊖⍤1)⍵ |
⌽⍵ |
reverse |
⍺(⊖⍤1)⍵ |
⍺⌽⍵ |
rotate (scalar ⍺) |
(f⌿⍤1)⍵ |
f/⍵ |
reduce |
(f⍀⍤1)⍵ |
f\⍵ |
scan |
Relative rank#
The right operand can also contain negative numbers, which are taken to be rank relative to the argument, rather than an absolute specification:
+/⍤¯1⊢3 3⍴⍳9 ⍝ Sum at rank one less than the rank of the matrix, i.e. along each row
]display 2 3 4⍴⍳24
]display +/⍤¯2⊢2 3 4⍴⍳24 ⍝ Sum at rank two less than the rank of the cube, i.e. along rows of each layer
Rank drills#
In his paper APL Excercises, Roger Hui sets out the following drills for Rank. See if you can predict the results before revealing the answers:
,t←2 3 4⍴⍳24
,⍤3⊢t
]DISPLAY ,⍤2⊢t
]DISPLAY ,⍤1⊢t
⊂⍤3⊢t
⊂⍤2⊢t
⊂⍤1⊢t
↑ ,¨ ⊂⍤3⊢t
]DISPLAY ↑ ,¨ ⊂⍤2⊢t
]DISPLAY ↑ ,¨ ⊂⍤1⊢t
]DISPLAY +⌿⍤3⊢t
]DISPLAY +⌿⍤2⊢t
]DISPLAY +⌿⍤1⊢t
]DISPLAY ⊖⍤3⊢t
]DISPLAY ⊖⍤2⊢t
]DISPLAY ⊖⍤1⊢t
If you got all those right, well done – Roger’s paper has got many more for you to pit your wits against.
Atop#
As we mentioned above, from version 18 of Dyalog, ⍤ can also be Atop if given a right operand function instead of array. We’ll see more of different kinds of Atop later in the tacit chapter, but for now it’s a functional composition rule, stating that (for the dyadic case),
X f⍤g Y → f X g Y
It is similar enough to Jot, ∘, to be confusing. Whilst monadic ∘ is an atop, dyadic ∘ is a beside. Behold:
f∘g X → f(gX) → fgX
f⍤g X → f(gX) → fgX
X f∘g Y → X f g Y
X f⍤g Y → f X g Y
Another way to think about it is that in the dyadic case, the difference between ∘ and ⍤ is which operand function (f or g) gets the left argument. In the monadic case, Atop is equivalent for ∘ and ⍤, so it’s worth using ⍤ for both monadic and dyadic atops for consistency.
Here is a simple example of a dyadic Atop,
1 2 3 -⍤+ 4 5 6 ⍝ Negate the sum of two vectors
which, following the X f⍤g Y → f X g Y rule, is the same as
-1 2 3+4 5 6 ⍝ Negate the sum of two vectors
or, as a tacit formulation (which we’ll cover in more detail later),
1 2 3 (-+) 4 5 6 ⍝ Negate the sum of two vectors