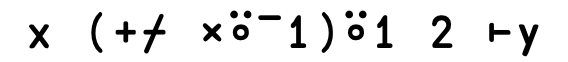Products
Contents
Products#
There is no point in being precise if you do not even know what you are talking about. –John von Neumann
⎕IO ← 0
]box on
]rows on
Was ON
Was OFF
We’ll talk about outer and inner products in APL, two powerful features. Other resources on these topics:
Mastering Dyalog APL has an excellent section on products, from around page 387.
Dyalog docs on outer product and inner product
Marshall Lochbaum’s talk on outer products
Outer product#
Let’s look at APL’s dyadic Outer product operator ∘. - and by “product” in this case we don’t mean multiplication, but as in outer product in the linear algebra sense. The canonical example of an outer product is to build a “times table”:
∘.×⍨⍳10
0 0 0 0 0 0 0 0 0 0 0 1 2 3 4 5 6 7 8 9 0 2 4 6 8 10 12 14 16 18 0 3 6 9 12 15 18 21 24 27 0 4 8 12 16 20 24 28 32 36 0 5 10 15 20 25 30 35 40 45 0 6 12 18 24 30 36 42 48 54 0 7 14 21 28 35 42 49 56 63 0 8 16 24 32 40 48 56 64 72 0 9 18 27 36 45 54 63 72 81
To all intents and purposes, that’s a nested for-loop which we could write out in Python along the lines of:
for j in range(10):
for i in range(10):
print(f"{i*j} ", end="")
print()
apart from the fact that in APL, outer products are vectorised and operate on the whole arrays.
The right side operand can be any dyadic function, including user-defined ones. For example:
∘.<⍨⍳10
0 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0
The eagle-eyed reader might interject that we can achieve the same thing with Rank:
(⍳10) <⍤0 1 ⊢ ⍳10
0 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0
If you realised that unprompted: well done – this is a deep insight.
Tip
Outer product can be defined in terms of Rank:
∘.f → f¨⍤0 99
The performance characteristics will differ though, for example
prod ← ∘.×
rank ← ×⍤0 1
x←⍳1000
]runtime -c "x prod x" "x rank x"
x prod x → 8.1E¯4 | 0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕ x rank x → 6.5E¯4 | -21% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕
Here’s an expression using an outer product that picks out the prime numbers between 0 and 20. Can you figure out how it works?
(2=+⌿0=x∘.|x)/x←⍳20
2 3 5 7 11 13 17 19
Inner product#
The Inner product, f.g is perhaps less obvious. An example of an inner product is actual matrix multiplication:
]DISPLAY A ← 3 4⍴3 2 0 8 11 7 5 1 4 9 6 10
]DISPLAY B ← 4 3⍴8 10 11 2 4 6 5 1 7 9 3 0
]DISPLAY A +.× B
┌→────────┐ ↓ 3 2 0 8│ │11 7 5 1│ │ 4 9 6 10│ └~────────┘
┌→──────┐ ↓8 10 11│ │2 4 6│ │5 1 7│ │9 3 0│ └~──────┘
┌→──────────┐ ↓100 62 45│ │136 146 198│ │170 112 140│ └~──────────┘
If you know how to multiply matrices, you’ll understand what the inner product operator does: consider the top left element of the result, 100. How did we get that? First we multiply each number in the first row of A with the corresponding element in the first col of B:
⎕ ← row0col0prod ← A[0;]×B[;0]
24 4 0 72
Then sum it:
+/row0col0prod
100
Next element:
+/A[0;]×B[;1]
62
We can apply inner product to many common problems where the impulse is to “first apply one function, then reduce another over the result”. For example, given two strings of equal lengths, how many letters are the same? You might try first:
+/'GATTACA' = 'TATTCAG' ⍝ Equal-then-sum-reduce
3
but this fits the inner product pattern nicely:
'GATTACA' +.= 'TATTCAG'
3
Calculating expected offspring#
Here’s a problem from Project Rosalind, a bioinformatics problem collection, Calculating Expected Offspring.
We’re given six integers, corresponding to the number of couples in a population possessing each genotype pairing for a given factor. In order, the six given integers represent the number of couples having the following genotypes:
AA-AA
AA-Aa
AA-aa
Aa-Aa
Aa-aa
aa-aa
If each couple have two offspring, what is the expected number of offspring displaying the dominant phenotype (A) in the next generation?
Let’s say we’re given the couples distribution as
data ← 19083 17341 19657 16896 16197 18256
I’m no biologist, but the way this works is that for each of the 6 possible genotype pairings we can see the probability of an offspring displaying the dominant phenotype, which is 1, 1, 1, 0.75, 0.5 and 0 respectively.
prob ← 1 1 1 0.75 0.5 0
We need to multiply the data with the corresponding probabilities, and sum that up, and finally multiply by 2, as we have two offspring per couple. This can be neatly formulated as an inner product:
2×data+.×prob ⍝ Same as 2× +/ data×prob
153703
eXplanation operator#
A handy trick when figuring out products is to use the “eXplanation” operator, that Adám Brudzewsky demonstrated in one of the Cultivations:
X ← {f←⍺⍺ ⋄ ⍺←⊢ ⋄ '(',⍺,(⎕CR'f'),⍵,')'} ⍝ The product eXplanation operator
Using this we can visualise how Dyalog will calculate each element in a product – inner and outer. For example, given
]DISPLAY A ← 2 3⍴6?20
]DISPLAY B ← 3 2⍴6?20
]DISPLAY A +.× B
┌→───────┐ ↓ 3 2 19│ │16 11 4│ └~───────┘
┌→────┐ ↓18 17│ │ 9 7│ │ 3 1│ └~────┘
┌→──────┐ ↓129 84│ │399 353│ └~──────┘
We can show how this was derived with X:
A +X.(×X) B
┌────────────────────────────────────┬────────────────────────────────────┐ │(( 3 × 18 )+(( 2 × 9 )+( 19 × 3 ))) │(( 3 × 17 )+(( 2 × 7 )+( 19 × 1 ))) │ ├────────────────────────────────────┼────────────────────────────────────┤ │(( 16 × 18 )+(( 11 × 9 )+( 4 × 3 )))│(( 16 × 17 )+(( 11 × 7 )+( 4 × 1 )))│ └────────────────────────────────────┴────────────────────────────────────┘