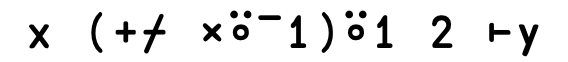The Över operator: ⍥#

Last week I was listening to a podcast on Hanselminutes, with Robert Martin talking about the SOLID principles… They all sounded to me like extremely bureaucratic programming that came from the mind of somebody that has not written a lot of code, frankly. –Joel Spolsky

If you thought rank looked startled, ⍤, wait until you meet his big sister, over: ⍥, nom de guerre for Circle Diaresis. Over was introduced to Dyalog in version 18. Over is a function composition rule, similar to those that govern tacit programming. Once you “see” this pattern, you’ll see it everywhere. Let’s take a look.

Over complements jot ∘ and the atop version of ⍤ in that it specifies how a set of functions should be applied to common arguments. If we compare f∘g and f⍤g, when given a left argument, ∘ gives it to the left-hand function and ⍤ gives it to the right-hand function. Other than that, they are the same. For the monadic case, these are all the same:

  • f∘g Y

  • f⍤g Y

  • f⍥g Y

In the dyadic case, look at the order of the leftmost two tokens:

  • X f∘g Y → X f g Y

  • X f⍤g Y → f X g Y

and over completes this by

  • X f⍥g Y → (g X)f(g Y)

Clear as mud? But this really is a common pattern. For example, let’s say we want to know if one vector is longer than another, we would previously have written:

X ← ⍳7
Y ← ⍳9
(≢X)>(≢Y)

0

Using over we can instead now write

X >⍥≢ Y

0

In words: first apply the right function to both arguments, then apply the left between the results. And of course, either side can be a user-defined function, too. Which vector have the most even numbers?

X >⍥{+/0=2|⍵} Y

0