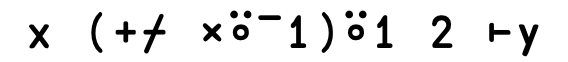Direct functions and operators
Contents
Direct functions and operators#
I made up the term “object-oriented,” and I can tell you I did not have C++ in mind. –Alan Kay
Until now, we’ve mainly used APL as a toolkit for array manipulation using its built-in primitives. Sure, it goes a long way, but to fully take advantage of it, we also need to be able to create our own functions and operators. Fortunately, the syntax – if we can even call it that – for user-defined functions, is super-simple. As someone said on the APL Orchard chat room, all you need to do is “slap curly braces around your code, and you’re done”. It’s not quite that simple, but not too far off.
The definition of a dfn (direct function) is enclosed in a pair of curly braces. It’s what’s known as an anonymous function, or a lambda, in other languages, meaning that there is no syntactic sugar for naming a function beyond ordinary assignment using Gets, ←:
name ← {
⍝ expressions
}
First a bit of unavoidable yak shaving: if a dfn fits entirely on a single line, you can type it out directly in the RIDE IDE. So far, so expected. If your dfn extends across multiple lines, you can’t (at the time of writing) just type it in. Dyalog is working on enhancing this.
Instead, the most convenient way to enter such a function is to say
)ed name
if you want to create a function called name. RIDE will open its function editor and let you enter your code there. Once you want to test your function, you first need to save it, which in APL-speak is called “to fix your function”. The default way (and you’re unlikely to ever discover this by yourself) to fix (save) your function is to hit esc. Yes, really. Fortunately – and I recommend you do so right now – RIDE allows you to re-bind keystrokes by clicking on the little keyboard symbol in the top-right corner.
Locate the row that says “Fix the current function” and map that to the key combo that is save on your platform. And whilst you’re there, make a note of the keys binding to “Forward” and “Backward” – they default to ctrl-shift-enter and ctrl-shift-backspace. In the REPL, these mean forward/back in the history of executed lines, like the arrow keys in the shell. The arrow keys instead move up and down spatially, in the output, still, to me an incomprehensible design decision. You might also want to rebind “Strong interrupt” to ctrl-c while you’re at it.
The other thing to note is that in RIDE there is no visual cue that an editor window contains unsaved changes. This is sure to bite you sooner or later.
In a Jupyter notebook, like here, entering functions might feel a bit more familiar: just type them into a cell. The only quirk is that in order to enter a multi-line dfn, you need to start the cell with ]dinput (which isn’t needed in a RIDE edit window). You can actually use the ]dinput way of entering a multi-line function in the interpreter REPL, too, but (in my opinion) it’s rather cumbersome unless you’re just cutting and pasting from somewhere else. In the upcoming (at the time of writing) version 18.1 there is experimental support for being able to type in multi-line functions directly in the REPL, similar to how that works in Python’s REPL.
First, our now familiar prelude:
⎕IO ← 0
]box on
]rows on
Was ON
Was OFF
We’re also going to make some assertions, so let’s have a helper function for that, courtesy of APL legend Roger Hui (and not speculating on its inner workings for now):
assert ← {⍺ ← 'assertion failure' ⋄ 0∊⍵: ⍺ ⎕signal 8 ⋄ shy ← 0}
Left and right arguments: ⍺, ⍵#
]dinput
MyFirstFunction ← {
⍝ Add left and right
⍺+⍵
}
32 MyFirstFunction 98
130
The first thing to note is the glyphs ⍺ and ⍵; the Greek letters alpha and omega. Alpha, the first letter of the Greek alphabet, is bound to the function’s left argument, and omega, the last letter of the Greek alphabet, is bound to the function’s right argument.
The second thing to learn is that APL expressions are separated by newline (or the diamond glyph, ⋄ which we’ll get to later). We could rewrite the above function to use an intermediate variable:
]dinput
Sum ← {
⍝ Add left and right
total ← ⍺+⍵
total
}
32 Sum 98
130
The third thing is that there is no “return” statement. The function returns the first non-assigned value. It’s worth letting this sink in: a function returns at the first point you do anything that isn’t an assignment. In the function above, the return point is us just stating the variable total.
Default left argument#
A useful feature is that you can set a default value for the left argument, ⍺. Compare:
{⍺ ← ¯99 ⋄ ⍺+⍵} 99
57 {⍺ ← ¯99 ⋄ ⍺+⍵} 99
0
156
This way a function can behave in different ways depending on if it is called monadically or dyadically. If you give a value to ⍺ with ←, then ⍺ will have this value if you didn’t pass a left argument to the function. On the other hand, if you do pass a left argument, the “alpha gets” line has no effect. When defaulting the left argument this way, note that this only works for the first time you give a value to alpha, which is perhaps obvious when you think of it:
{⍺ ← ¯99 ⋄ ⍺ ← ¯999999 ⋄ ⍺+⍵} 99
0
Setting a default value for the left argument is a useful tool if you write recursive dfns, which typically accumulate their result on the left argument. This way you can call the function monadically to start, but subsequent iterations can use the left argument to build up the result. We’ll talk more about recursion later in the chapter on iteration techniques, but here’s a taster to demonstrate the default left argument technique. The glyph Del (∇) is a reference to the innermost function:
]dinput
sum ← {
⍺ ← 0 ⍝ Initialise the accumulator
0=≢⍵:⍺ ⍝ If right arg empty vector, return accumulator, see below!
(⍺+⊃⍵)∇1↓⍵ ⍝ Add head to accumulator, recurse over tail
}
sum ⍳10
100 sum ⍳10
45
145
Alternation#
What about alternation? We got a brief view of a conditional return in the example just above – a guard statement. Recall that there is no if-statement for us. A guard, defined with a colon, says, if the expression to the left of the colon is true, return from the function with the value to the right of the colon. A contrived example:
]dinput
Palinish ← {
rev ← ⊖⍵ ⍝ Reverse the right arg
rev≡⍵: 1 ⍝ If right arg matches its own reverse, return 1
0 ⍝ Else, return 0
}
Palinish 1 2 3 2 1
Palinish 1 2 3 4 5
Palinish 3
1
0
1
For the avoidance of doubt, we could of course have written that as
{⍵≡⊖⍵} 1 2 3 2 1 ⍝ Anonymous (unnamed) version
1
Note that execution flow does not carry on after a guard expression, even if that was an assignment. This requires some thought when writing code that needs to conditionally “do something” and then carry on, as illustrated in the following meaningless Python-like snippet:
def foo(arg):
fum = 57
fee = 8
if flerp(arg) < 47:
fee = 92
fum = flumm(arg)
return fee + fum
Actually, we can turn that into APL trivially, using only what we already know:
foo ← {47>flerp ⍵: 92+flumm ⍵ ⋄ 57+8} ⍝ Note: diamond separator
Let’s investigate some possible patterns for achieving a flow where execution carries on following an “if-then-else” branch. On way is to use an anonymous function, in essence like Python’s
a = 42 if answer else -99
]dinput
foo ← {
answer ← ⍵
a ← {⍵:42 ⋄ ¯99} answer
⍝ ...execution follows here
⍝ do something with a
}
In this case, as answer is a boolean, we could have avoided the inner function entirely by simply picking the values from a 2-element vector (note: need ⎕IO←0 for this to work):
]dinput
foo ← {⎕IO←0
answer ← ⍵
a ← answer⊃¯99 42
⍝ ...execution follows here
⍝ do something with a
}
With the first technique (the anonymous function) we have scope to extend the work done in each branch by making the function more complex, but ultimately it still returns a value. What if we need to modify multiple values? We could of course return an array of things, that’s a perfectly valid approach.
Name scoping rules in Dyalog are a mixture between dynamic and lexical scope. Here’s what Dyalog’s docs say about it:
When an inner (nested) dfn refers to a name, the interpreter searches for it by looking outwards through enclosing dfns, rather than searching back along the state indicator.
Lexical scope is almost certainly “what you expect”. However, as Dyalog has no dedicated syntax for declaring a variable beyond giving it a value, if you need to modify a variable not introduced in the innermost dfn, we need a way to indicate this.
Consider the following:
]dinput
foo ← {
a ← 45
_ ← {a←¯99}⍬
a
}
foo ⍬ ⍝ Note: 45, not ¯99
45
The innermost function creates a new variable with lexical scope, with the name a. So how do you modify state defined outside a function? This is where modified assignment comes in.
Modified Assignment#
Modified assignment should feel familiar to any C or Python programmers amongst you:
# Modified assignment, Python-style
a = 45
a += 45 # a is now 90
In APL, we can also modify an existing variable’s value via a function, for example:
]dinput
foo ← {
a ← 45
_ ← {a +← 45}⍬
a
}
⎕ ← r ← foo ⍬
assert r=90
90
The supremely useful, but perhaps non-intuitive kicker: you can use modified assignment with Right tack (⊢) to set values:
]dinput
foo ← {
a ← 45
_ ← {a ⊢← ¯99}⍬
a
}
⎕ ← r ← foo ⍬
assert r=¯99
¯99
We’ve already met a bunch of selectable assignment expressions when we talked about indexing. We can use all of those here. For example, we can mutate cells in a matrix using bracket indexing:
]dinput
foo ← {
a ← 3 3⍴1 ⍝ 3×3 matrix of all 1
_ ← {a[1;1] ← 0}⍬
a
}
⎕ ← r ← foo ⍬
assert r≡3 3⍴1 1 1 1 0 1 1 1 1
1 1 1 1 0 1 1 1 1
Direct operators#
We’ve met some of APL’s built-in operators already, like Reduce and Selfie. Operators are perhaps the closest APL gets to the functional programming paradigm. An operator is a function that returns a derived function. An operator can take other functions as its operands.
Consider Reduce, /. It’s a monadic operator that returns a derived function that can be called both monadically and dyadically:
2 (+/) ⍳10 ⍝ Parentheses not required, added for illustrative purposes
1 3 5 7 9 11 13 15 17
Here we see the monadic reduction operator, its sole operand being the plus function. The derived function it returns, plus-reduce, is called dyadically, with 2 to its left and ⍳10 to its right. In this case, a windowed reduction. We could have said
sumred ← +/
2 sumred ⍳10
1 3 5 7 9 11 13 15 17
to emphasize the fact that the operator really returns a function.
Dyalog lets us write our own operators, too, in a very similar way to how we write dfns. We call our own operators direct operators, henceforth just dops. Operators can be powerful, but the need for them actually rarely arises in practice. The reason for this is that the built-in operators already let you apply your own functions in various ways.
A few things to note with operators:
In a dop,
⍺⍺represents the left operand, and⍵⍵is the right operand.Unlike a monadic dfn, which takes a right argument, a monadic dop takes a left argument, like we just saw in the case of reduce.
The operator can refer to itself for recursion using
∇∇, analogously to the dfn’s∇.
Here’s an example monadic dop from the dfns workspace, a left-to-right version of reduce:
]dinput
foldl ← { ⍝ Fold (reduce) from the left.
⍺ ← ⊃0⍴⍵ ⍝ Default initial value for accumulator
↑⍺⍺⍨/(⌽⍵),⊂⍺
}
This implements foldl in terms of the standard foldr by reversing the list and appending an accumulator element.
+foldl ⍳10
+/⍳10
-foldl ⍳10
-/⍳10
45
45
¯45
¯5
This version takes an optional left argument that can be used to initialise the accumulator:
99 +foldl ⍳10
144
Whilst there isn’t anything overly complex about writing your own operators as such, we probably won’t need to use many of them for the rest of this book, but at least now you have seen them.