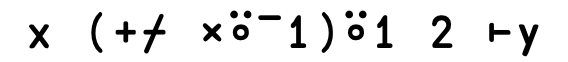Iteration
Contents
Iteration#
As long as I’m alive, APL will never be used in Munich –Fritz Bauer
Nor in Holland –Edsger Dijkstra (as told by Alan Perlis)
We started all this by claiming that there are no loops in APL. This is of course not entirely true: there are plenty of ways of achieving iteration, some of which are more efficient than others.
In order to get the best possible performance out of APL, it’s worth seeking data-parallel algorithms, typically employing Boolean masks. However, it’s not always possible, or sometimes performance matters less than code complexity, and a more iterative solution can be both clearer and fast enough.
We have at least four, maybe five different kinds of iteration mechanisms at our disposal: Each (¨), Reduce (⌿), Del (∇) and Power (⍣). The fifth is that of scalar pervasion, which can either be seen as a way of achieving iteration, or as a way of avoiding iteration, depending on your point of view. Wait, is it six? Maybe we should count Rank (⍤), too? Rank deserves its own separate section! Oh, and Scan (⍀), don’t forget Scan!
Let’s introduce them.
⎕IO ← 0
]box on
]rows on
assert ← {⍺ ← 'assertion failure' ⋄ 0∊⍵: ⍺ ⎕signal 8 ⋄ shy ← 0}
Was ON
Was OFF
Each (a.k.a map): ¨#
Most languages nowadays have a map construct. In fact, it’s occasionally touted – erroneously – as sufficient evidence that a language is “functional” if it has a map function.
Perhaps you’ve seen Python’s somewhat cumbersome version of map:
>>> list(map(lambda x: x*x, [1, 2, 3, 4, 5, 6, 7, 8, 9])) # Square elements
[1, 4, 9, 16, 25, 36, 49, 64, 81]
which in Python corresponds to something like
def mymap(func, iterable):
for item in iterable:
yield func(item)
Of course, seasoned Pythonistas would rightly frown at the above and instead recommend a list comprehension.
A map takes a function and applies it to every element in an array, creating a result array of the same length as its argument.
In APL, the glyph for map – referred to as Each – is two high dots: ¨.
×⍨¨1+⍳9 ⍝ Square elements via each (but see below!)
1 4 9 16 25 36 49 64 81
This wasn’t actually a great example, this is one of those cases where using a scalar function already does the job for us:
×⍨1+⍳9 ⍝ Square elements via scalar pervasion
1 4 9 16 25 36 49 64 81
Scalar pervasion means that functions in certain cases already know how to penetrate arrays.
Let’s try another. Given a nested vector, what are the lengths of the elements?
⎕ ← V ← (1 2 3 4)(1 2)(3 4 5 6 7)(,2)(5 4 3 2 1)
≢¨V ⍝ Tally-each
┌───────┬───┬─────────┬─┬─────────┐ │1 2 3 4│1 2│3 4 5 6 7│2│5 4 3 2 1│ └───────┴───┴─────────┴─┴─────────┘
4 2 5 1 5
If you’re used to a different language, Each has a seductive quality, as it maps conceptually onto constructs you already know how to use. Beware though that in APL it’s often inefficient, and that there are usually better alternatives.
Reduce (a.k.a foldr): ⌿, /#
Most languages today sport some kind of variety of fold or reduce, regardless of the level of “functional” they claim to be.
In APL, Reduce is a central feature, which somewhat unhelpfully hijacks the glyph also used by Compress/Replicate, /. This is one, albeit not the main, reason why we prefer to use its close cousin, Reduce first, ⌿, where we can. Reduction has a bit of an unfair reputation of being hard to understand. Guido reportedly hates reduce() in Python so much that it was demoted down to the dusty functools module:
So now reduce(). This is actually the one I’ve always hated most, because, apart from a few examples involving + or *, almost every time I see a reduce() call with a non-trivial function argument, I need to grab pen and paper to diagram what’s actually being fed into that function before I understand what the reduce() is supposed to do. So in my mind, the applicability of reduce() is pretty much limited to associative operators, and in all other cases it’s better to write out the accumulation loop explicitly. –Guido van Rossum
Despite what Guido thinks, reduction is actually a pretty simple idea, and APL may even have been the first programming language with reduce in it (some Lispers disagree). Think of the operation of summing a bunch of numbers – this is an example of a reduction.
In APL, Reduce applies a function to elements in an array, producing a result which is rank-reduced by 1. In other words, reducing a vector (rank 1) produces a scalar (rank 0). In the example of +, summing the elements of a vector obviously produces a scalar: the total.
+⌿1 2 3 4 5 6 7 8 9 ⍝ sum-reduce-first integers 1-9
45
Simplifying a bit, we can think of Reduce first as an operator that injects its left operand function in the gaps between elements of the argument:
1+2+3+4+5+6+7+8+9
45
When using Reduce in APL, you need to take extra care to ensure that it works with its strict right to left evaluation order. A reduce is also called a fold in other languages (Lisp, Erlang etc), and APL’s Reduce is a so-called foldr – it reduces right to left, which makes sense for APL, but occasionally less sense for the programmer.
Again, it can help writing it out in long-hand to see what’s going on:
-⌿1 2 3 4 5 6 7 8 9 ⍝ difference-reduction -- take care: right to left fold!
5
If that was the result you expected, you’re well on your way to mastery. Inject the operand between items:
1-2-3-4-5-6-7-8-9
5
Reduction is especially useful when working with higher-rank arrays. Reduce first is called so because it reduces along the first axis. So a sum-reduce-first of a rank 2 integer array will sum its columns to produce a vector (rank 1) of the columnar sums:
⎕ ← m ← 3 3⍴9?9
+⌿m
3 0 5 4 1 8 6 7 2
13 8 15
If we wanted to sum-reduce along the rows, we can either use / (which for historical reasons does just that):
+/m
8 13 15
or we can explicitly tell ⌿ to apply along a different axis, using bracket axis:
+⌿[1]m
8 13 15
For consistency, it’s best to prefer operators and functions that default to applying to the leading axis where possible. The fact that APL, unlike J, has a mixture is an unhelpful side-effect of backwards compatibility.
Windowed reduction#
Reduce has a few more handy tricks up its sleeve. Instead of reducing the whole argument array, we can employ a sliding window. This lets us compute a set of reductions over shorter stretches of the data. The derived function returned by the reduction operators can be called dyadically, specifying as the left argument the size of the sliding window.
For example, to calculate the sum of each element in a vector with its subsequent element, we employ a reduction with a sliding window of size 2:
2+⌿1 2 3 4 5 6 7 8 9
3 5 7 9 11 13 15 17
Scan: \, ⍀#
Scan/Scan first blurrs the distinction between Each and Reduce. In right hands, it can be a true APL super power, but beware that scans tend to be slow: most scans run to O(n²), although the interpreter can optimise some to the O(n) you perhaps expected.
Scan is just like Reduce, but instead returns every intermediate state, not just the end state. A sum-reduce of a vector of numbers returns the sum total. A sum-scan of the same vector returns the running sums:
+⌿1 2 3 4 5 6 7 8 9 ⍝ Sum-reduce first
+⍀1 2 3 4 5 6 7 8 9 ⍝ Sum-scan first
45
1 3 6 10 15 21 28 36 45
One way we can think of scan is that it’s the amalgamation of all possible calls to Reduce with the same operand, taking in increasing lengths of the argument array. In the case above:
+⌿1
+⌿1 2
+⌿1 2 3
+⌿1 2 3 4
+⌿1 2 3 4 5
+⌿1 2 3 4 5 6
+⌿1 2 3 4 5 6 7
+⌿1 2 3 4 5 6 7 8
+⌿1 2 3 4 5 6 7 8 9
1
3
6
10
15
21
28
36
45
As with Reduce, it’s worth re-emphasizing that Scan still is evaluated right-to-left, as with everything else APL, no matter how much you’d prefer it to run left to right instead. You can, of course, roll your own scan-left if you really need it.
Power: ⍣#
One of my favourite glyphs! It looks like a happy starfish! The Power operator is… powerful. Conceptually it should be easy to grasp, but there are some aspects that take time to understand. Formally, it’s defined as a function repeatedly applied to the output of itself, until some stopping criterion is fulfilled. If you pass it an integer as its right operand, it’s basically a for-loop:
f ← { ... } ⍝ some function or other
f f f f f f f f argvector ⍝ repeatedly apply function to itself, eh 8 times
f⍣8 ⊢ argvector ⍝ power-8
If you give it a function as the right operand, it can be used as a while-loop. One example is to find a function’s fixed point:
2÷⍨⍣=10 ⍝ Divide by 2 until we reach a fixed point
0
Here the right operand function is equals =. This says: repeatedly apply the left operand (2÷⍨) until two subsequent applications return the same value.
We can explicitly refer to the left and right arguments of the right operand function. The left argument, ⍺, refers to the result of the function application to the right argument, ⍵.
Keep generating random numbers between 1 and 10 until we get a 6:
{⍞ ← ?10}⍣{6=⍺} 0 ⍝ Keep generating random numbers between 1 and 10 until we get a 6
1991487931157990989988905581516 6
The Quad-quote-gets (⍞←) combo prints values without newlines. The final result is also returned, the expected 6.
Del: ∇#
Dyalog has a most excellent, concise and efficient recursion operator, ∇. It allows you to express recursive algorithms in a natural, almost Lisp-like fashion. The interpreter has a very good TCO implementation.
Let’s start with making our own version of sum-reduce, this time without actually using the Reduce operator.
]dinput
Sum ← {
⍺ ← 0 ⍝ Left arg defaults to 0 if not given
0=≢⍵: ⍺ ⍝ If right arg is empty, return left arg
(⍺+⊃⍵)∇1↓⍵ ⍝ Add head to acc, recur over tail
}
⎕ ← mysum ← Sum 1 2 3 4 5 6 7 8 9
assert mysum=+/1 2 3 4 5 6 7 8 9
45
Yup, that seems to work; good.
The glyph Del (∇) is a reference to the current innermost dfn. If your dfn has a name, you can substitute it for the actual function name. In our case, the last line could equally well have been written:
(⍺+⊃⍵)Sum 1↓⍵
However, using the glyph has a number of advantages: it’s more concise, immune to function name changes, and works equally well for anonymous dfns.
Our Sum dfn follows a common pattern: we accumulate something as the left argument, and decrease the right argument, either by magnitude, or as in this case, by dropping items off the front of a vector.
The recursion termination guard,
0=≢⍵: ⍺
simply states that, if the right argument is empty, we should return our accumulator. The recursive call itself is:
Add the head of the right argument to the accumulator.
Recur with the updated accumulator as the new left argument and with the tail as the right argument.
If the last thing the function does is a function call, and this includes Del, this is what’s called a tail call which the Dyalog interpreter can handle without the addition of an extra stack frame. If you’re using Del, strive to make all your recursive functions tail calls – avoid making your function do any work on the value you get back from the recurring line – for example, note that 1+⍺∇⍵ isn’t a tail call, as the last thing that happens is the 1+... not the ⍺∇⍵.
For a fractionally more involved example, let’s write our own sum-scan.
]dinput
Sscan ← {
⍺ ← ⍬ ⍝ Left arg defaults to ⍬ if not given
0=≢⍵: ⍺ ⍝ If right arg is empty, return left arg
(⍺,⊃⍵+⊃¯1↑⍺)∇1↓⍵ ⍝ Append the sum of the head and the last element of acc and recur on tail
}
⎕ ← myscan ← Sscan 1 2 3 4 5 6 7 8 9
assert myscan≡+⍀1 2 3 4 5 6 7 8 9
1 3 6 10 15 21 28 36 45
No discourse on recursion is complete without mentioning the Fibonacci sequence. You know which one I mean – every number is the sum of its two direct predecessors:
0 1 1 2 3 5 8 13 21 34 ⍝ etc, something about rabbits
Here’s one possible formulation where the right argument is the Fibonacci ordinal.
]dinput
Fib ← { ⍝ Tail-recursive Fibonacci.
⍺ ← 0 1
⍵=0: ⊃⍺
(1↓⍺,+/⍺)∇⍵-1
}
Fib¨⍳10 ⍝ The 10 first Fibonacci numbers
0 1 1 2 3 5 8 13 21 34
The pattern is still the same: set a default for the accumulator, ⍺. Terminate on some condition on ⍵, returning a function of the accumulator. Modify the accumulator, given the head of the right argument, and recur on the tail.
The guts of the function is the last line. To the right, we decrease the right argument – this is our loop counter if you like. To the left is our accumulator, which basically is a sliding window of size 2 over the Fib sequence. We append the sum of the two numbers, and drop the first, and recur over the tail.
Here’s a pretty neat implementation of the Quicksort algorithm:
]dinput
Quicksort ← {
1≥≢⍵: ⍵
S ← {⍺⌿⍨⍺ ⍺⍺ ⍵}
⍵((∇<S),=S,(∇>S))⍵⌷⍨?≢⍵
}
Here ⍵⌷⍨?≢⍵ is the pivot element, picked at random, and the S operator partitions its left argument array based on its left operand function and the pivot element to the right. The whole idea of quicksort is pretty clearly visible in the tacit fork (∇<S),=S,(∇>S) – elements less than the pivot, the pivot, elements greater than the pivot, recursively applied.
Quicksort ⎕←20?20
3 10 4 15 9 11 0 7 6 14 13 5 2 19 18 12 8 1 17 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
Another example is binary search: locate an element in an array that is known to be sorted. Here’s a function to do that:
]dinput
bsearch ← {⎕IO←0
_bs_ ← { ⍝ Operator: ⍺,⍵ - lower,upper index. ⍺⍺ - item, ⍵⍵ - array
⍺>⍵: ⍬ ⍝ If lower index has moved past upper, item's not present
mid ← ⌈0.5×⍺+⍵ ⍝ New midpoint
⍺⍺=mid⊃⍵⍵: mid ⍝ Check if item is at the new midpoint
⍺⍺<mid⊃⍵⍵: ⍺∇¯1+mid ⍝ Drill into lower half
⍵∇⍨1+mid ⍝ Upper half
}
0 (⍺ _bs_ (,⍵)) ¯1+≢,⍵
}
5 bsearch 0 2 3 5 8 12 75
5 bsearch 0 2 3 5 8 12
5 bsearch 5 5
5 bsearch 5
]display 1 bsearch 0 2 3 5 8 12
3
3
1
0
┌⊖┐ │0│ └~┘
Performance considerations#
The pattern we’ve used in some of the examples above,
⍝ some stuff
0=≢⍵:⍺
head ← 1↑⍵
tail ← 1↓⍵
(head f ⍺)∇tail
has a …sting in the tail, especially if you come from a functional language where that pattern is the expectation, like Racket, Erlang or Clojure. In such languages, vectors/lists are either implemented as linked lists, slices, or are immutable, meaning that dropping an element from the front is an O(1) operation. In APL, like in Python, that’s an O(n) operation. When combined with recursion, this can be crushing for performance. Here’s an example.
The Knuth-Morris-Pratt algorithm is an efficient string search algorithm. In one of its forms it pre-calculates a prefix table, which is a metric of how well a string matches against shifts of itself. The brilliant.org article linked to above has this written out in Python as:
def prefix(p):
# https://brilliant.org/wiki/knuth-morris-pratt-algorithm/
m=len(p)
pi=[0]*m
j=0
for i in range(1,m):
while j>=0 and p[j]!=p[i]:
if j-1>=0:
j=pi[j-1]
else:
j=-1
j+=1
pi[i]=j
return pi
Here’s an example running that:
Stefans-MacBook-Pro:~ stefan$ python
Python 3.8.5 (default, Sep 17 2020, 11:24:17)
[Clang 11.0.3 (clang-1103.0.32.62)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> from kmp import prefix
>>> prefix('CAGCATGGTATCACAGCAGAG')
[0, 0, 0, 1, 2, 0, 0, 0, 0, 0, 0, 1, 2, 1, 2, 3, 4, 5, 3, 0, 0]
>>>
We can write that as an APL dfn like so:
]dinput
prefix1 ← {⎕IO←0
p ← ⍵
pi ← 0⍴⍨≢⍵
j ← 0
{
0=≢⍵: pi
i ← ⊃⍵ ⍝ head
pi[i] ← j⊢←1+{⍵<0:⍵⋄p[⍵]=p[i]:⍵⋄0≤⍵-1:∇pi[⍵-1]⋄¯1} j ⍝ while j>=0 and p[j] != p[i]
∇1↓⍵ ⍝ tail
} 1+⍳¯1+≢⍵ ⍝ for i in range(1, m)
}
and we’d hope it produces the same result:
prefix1 'CAGCATGGTATCACAGCAGAG'
0 0 0 1 2 0 0 0 0 0 0 1 2 1 2 3 4 5 3 0 0
So that’s two nested “loops”, both nicely tail recursive, and probably similar to how you’d construct it in Clojure or Racket. However, as the argument string grows, the performance tanks. We can illustrate this by tweaking it a tiny bit to avoid the reallocation of the argument to the recursive call in the outer loop:
]dinput
prefix2 ← {⎕IO←0
p ← ⍵
pi ← 0⍴⍨≢⍵
j ← 0
0 {
⍺=≢⍵: pi
i ← ⍺⊃⍵ ⍝ Note: pick ⍺, not first
pi[i] ← j⊢←1+{⍵<0:⍵ ⋄ p[⍵]=p[i]:⍵ ⋄ 0≤⍵-1:∇ pi[⍵-1] ⋄ ¯1} j
(⍺+1)∇ ⍵ ⍝ Note: no tail!
} 1+⍳¯1+≢⍵
}
Instead of taking the tail of ⍵, we pass the current index as ⍺. Let’s see if that works before we proceed:
prefix2 'CAGCATGGTATCACAGCAGAG'
0 0 0 1 2 0 0 0 0 0 0 1 2 1 2 3 4 5 3 0 0
To demonstrate the difference, let’s compare performance on a long string. Here’s one taken from Project Rosalind:
data ← ⊃⊃⎕NGET'../kmp.txt'1 ⍝ From http://rosalind.info/problems/kmp/
≢data ⍝ LONG STRING!
99972
'cmpx'⎕CY'dfns' ⍝ Load `cmpx` - comparative benchmarking
cmpx 'prefix1 data' 'prefix2 data'
prefix1 data → 9.7E¯1 | 0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕ prefix2 data → 1.5E¯1 | -85% ⎕⎕⎕⎕⎕⎕
Quite a staggering difference for such an innocuous change, perhaps.
The binary search implementation we concluded the previous section with already ‘does the right thing’ – it doesn’t cut off the data array on each iteration. So it should be fast, right? Searching for a number amongst a hundred thousand or so must be faster than the APL primitive function that examines every element looking for a match. Surely…? In Algorithms 101 they taught you that O(log n) always beats O(n)!
Except when it doesn’t:
data ← ⍳100000 ⍝ A loooot of numbers
cmpx 'data ⍳ 17777' '17777 bsearch data' ⍝ Look for the number 17777
data ⍳ 17777 → 5.2E¯6 | 0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕ 17777 bsearch data → 1.1E¯5 | +112% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕
Ouch… a lesson for the APL neophyte here. Your intuition for what’s efficient and what isn’t is almost certainly wrong. But wait, we can do even better. Let’s have a randomised array for APL to go at:
randInts ← 100000 ? 100000
cmpx 'randInts⍳1' 'randInts⍳19326' 'randInts⍳46729'
randInts⍳1 → 2.6E¯5 | 0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕ * randInts⍳19326 → 7.0E¯6 | -73% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕ * randInts⍳46729 → 2.2E¯6 | -92% ⎕⎕⎕
We can make this even faster by pre-binding the array to the Index Of function:
find←randInts∘⍳
cmpx 'find 1' 'find 19326' 'find 46729'
find 1 → 1.1E¯7 | 0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕ * find 19326 → 1.1E¯7 | -1% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕ * find 46729 → 1.1E¯7 | -1% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕
What’s happening there is that Dyalog takes the binding to mean that as the lookup array is now fixed, it can make a hashed index behind the scenes. You can see that the times taken don’t vary much with the argument.
But there is more performance to squeeze out here. If our search array is ordered, we can use Interval Index, dyadic ⍸, as a binary search (which it is!):
cmpx 'data⍸1' 'data⍸19326' 'data⍸46729'
data⍸1 → 1.2E¯4 | 0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕ * data⍸19326 → 1.2E¯4 | 0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕ * data⍸46729 → 1.2E¯4 | -1% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕
Interval Index is very optimised in the 18.0/1 versions of Dyalog. Sadly, this optimisation had to be dropped in 18.2.
Key point: simple APL primitives on simple arrays are always faster than anything you can write in APL. Only ever iterate or recurse if there are no other alternatives.
Exercise for the reader: as the data grows, sooner or later the bsearch function will win out. How large does the array need to be for that to happen?
Scalar pervasion#
We touched briefly on scalar pervasion above, but it’s an important topic, so let’s dive in a little bit deeper. It’s worth reading what Dyalog has to say on the topic in the docs.
The idea is that a certain class of functions is pervasive. This means that a function that operates on a scalar will operate on scalars at any level of nesting if applied to an array. Recall that the level of nesting is not the same as the rank in APL.
Consider a nested vector that contains both numbers and other vectors of numbers:
⎕ ← nesty ← (1 2 3 (3 4 (5 6)) 7)
┌─┬─┬─┬─────────┬─┐ │1│2│3│┌─┬─┬───┐│7│ │ │ │ ││3│4│5 6││ │ │ │ │ │└─┴─┴───┘│ │ └─┴─┴─┴─────────┴─┘
As an obvious and simple example, let’s say we want to negate all the numbers:
-nesty
┌──┬──┬──┬─────────────┬──┐ │¯1│¯2│¯3│┌──┬──┬─────┐│¯7│ │ │ │ ││¯3│¯4│¯5 ¯6││ │ │ │ │ │└──┴──┴─────┘│ │ └──┴──┴──┴─────────────┴──┘
Where it can be applied, scalar pervasion is an efficient operation in Dyalog APL. It works for dyads, too:
(1 2) 3 + 4 (5 6)
(1 1⍴5) - 1 (2 3)
┌───┬───┐ │5 6│8 9│ └───┴───┘
┌─┬───┐ │4│3 2│ └─┴───┘