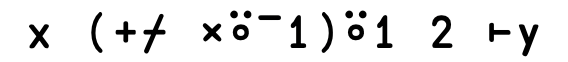Encode decode: ⊤⊥
Contents
Encode decode: ⊤⊥#
Teaching peers is one of the best ways to develop mastery. –Jeff Atwood
Here’s some of APL’s secret sauce, not commonly encountered in other languages: Encode, ⊤ and Decode, ⊥. Encode and Decode provide efficient basis conversion across potentially mixed radixes.
Other resources:
⎕IO ← 0 ⍝ You know the drill
The canonical example is to convert numbers between bases, for example, converting a base-10 number to 8-bit binary:
(8⍴2)⊤54
0 0 1 1 0 1 1 0
…and back to base-10:
2⊥0 0 1 1 0 1 1 0
54
I vowed not to mention magic inverses, but these few are too damned useful to leave out. Convert a base-10 number to binary, using the least number of bits:
2∘⊥⍣¯1 ⊢ 54
1 1 0 1 1 0
…and as a consequence, split a number into its constituent digits:
10∘⊥⍣¯1 ⊢ 677398723 ⍝ Number to digit vector
6 7 7 3 9 8 7 2 3
Those were all fixed radix. An example of mixed radix is converting between seconds and days, hours, mins and seconds, e.g “how many days, hours, mins and seconds is 10000 seconds”?
1 24 60 60⊤10000
0 2 46 40
and, conversely, how many seconds in 1 day (and night)?
1 24 60 60⊥1 0 0 0
86400
Here’s an example of Decode and Encode, borrowed from Mathematica’s documentation for its corresponding MixedRadix function.
A Roman legion was made of 10 cohorts, a cohort of 6 centuries, a century of 10 contuberniae, and a contubernia of 8 soldiers.
units ← 'legion' 'cohort' 'century' 'contubernia' 'soldier'
bases ← 10 10 6 10 8
Given 16,894 soldiers, how are they organized?
↑units (bases⊤16894)
┌──────┬──────┬───────┬───────────┬───────┐ │legion│cohort│century│contubernia│soldier│ ├──────┼──────┼───────┼───────────┼───────┤ │3 │5 │1 │1 │6 │ └──────┴──────┴───────┴───────────┴───────┘
Going the other way, how many soldiers are there in a legion?
bases⊥1 0 0 0 0
4800
Decode has some less obvious uses, too. For example, we can use 1⊥ to sum vectors:
1⊥⍳10
45
The utility of that may not be obvious, but it comes very handy when writing tacit code which we’ll cover in depth later, but here’s a taster – given a vector where all elements are the same, bar one, what’s the index of the “odd one out”?
(1⍳⍨1⊥∘.=⍨) 243 243 243 243 251 243 243 ⍝ Index of "odd one out"
4
The enigmatic ⊥⍨ counts trailing 1s:
⊥⍨0 1 0 0 1 1 0 1 1 1 1 1
5
We can also use Encode and Decode between indices of an array and its ravel:
⎕ ← m ← 3 5 ⍴15?15
⎕ ← rav ← ,m
3 0 5 12 4 9 8 6 2 10 11 7 1 14 13
3 0 5 12 4 9 8 6 2 10 11 7 1 14 13
Given index ← 1 4 into the above array, what’s the corresponding index into the ravel vector?
index ← 1 4
⎕ ← k ← (⍴m)⊥index ⍝ 2D to 1D
m[⊂index]
k⊃rav
9
10
10
And the reverse:
⎕ ← i j←(⍴m)⊤k ⍝ 1D to 2D
1 4
Higher ranks#
So far, we only used vectors as arguments to Encode and Decode. However, they can take arguments of higher ranks, too. It may not be immediately obvious what this means, so let’s look at that.
Encode returns an array where the shape is the combined shape of the left and right arguments:
24 60 60⊤5000 10000 15000 20000 ⍝ Convert 5000 10000 15000 20000 to HMS
1 2 4 5 23 46 10 33 20 40 0 20
So the shape is 3 4. If we apply the same operation to a matrix, the same relationship holds:
seconds ← ⎕ ← 2 2⍴5000 10000 15000 20000
24 60 60⊤seconds
5000 10000 15000 20000
1 2 4 5 23 46 10 33 20 40 0 20
Again, the shape is 3 layers (as 3=≢24 60 60) of shape 2 2. The leading axis holds the results which is easier to see with a transpose applied:
⎕IO←0
2 0 1⍉24 60 60⊤seconds
1 23 20 2 46 40 4 10 0 5 33 20
Perhaps more surprisingly, we can use a higher-ranked argument to the left, too. It then provides multiple radix vectors into which to encode the right hand side. Let’s say we want to convert a set of numbers to bases 10 and 16:
radix ← ⎕ ← 3 2⍴10 16
radix⊤128 256
10 16 10 16 10 16
1 2 0 1 2 5 8 0 8 6 0 0
We expected the shape 3 2 2, but perhaps it’s tricky to untangle why the result looks like it does. It’s essentially an outer product, with a different axis order:
⍉↑⍉(10 10 10)(16 16 16)∘.⊤128 256
1 2 0 1 2 5 8 0 8 6 0 0
⍉(3 2⍴10 16)⊤128 256
1 2 8 0 8 0 2 5 6 1 0 0
which is
128 = (1,2,8)₁₀
128 = (0,8,0)₁₆
256 = (2,5,6)₁₀
256 = (1,0,0)₁₆
Higher ranks for both left and right left as an exercise for the interested reader.